第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
第五单元探究性作业
第五单元探究性作业 数线段和角
本单元我们已经学习了线和角,我们知道:2个点最多可以连出1条线段,那么3个点,4个点……最多可以连出多少条线段呢?让我们一起探究一下吧!
【问题探究】
1. 下图中的2个点、3个点、4个点、5个点……分别最多可以连出几条线段?

【分析探究】
方法1 选中一个点,向其他点分别连线。
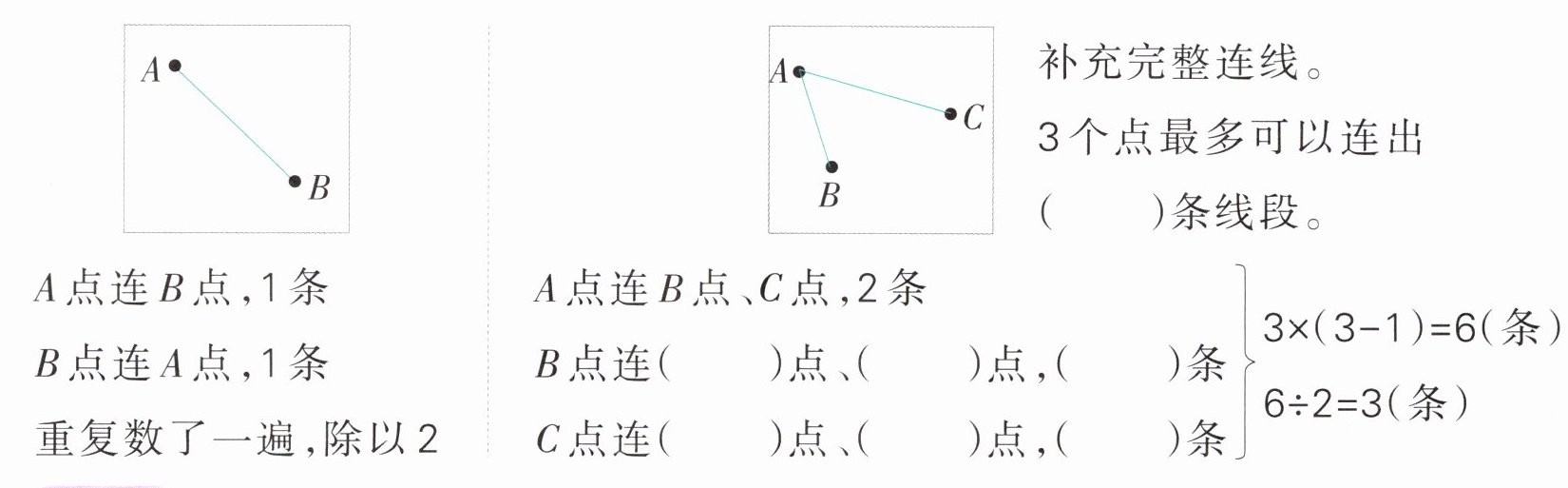
方法2 依次连线,不连重复的。
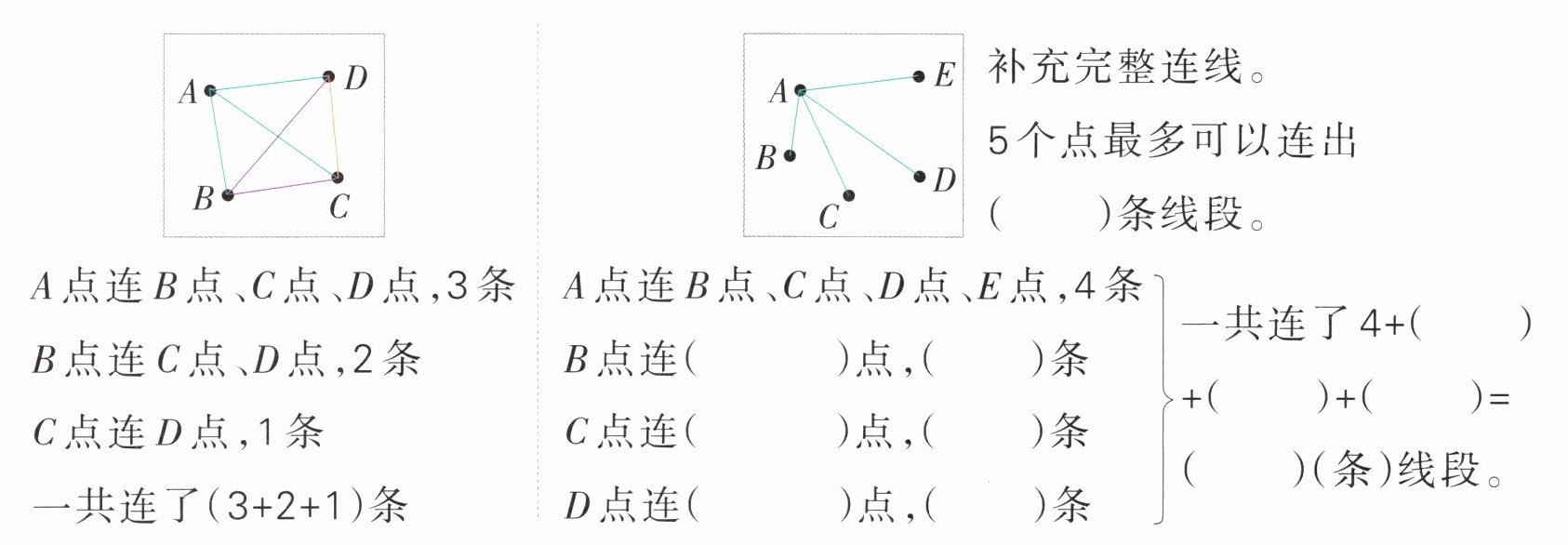
【规范解答】
【探索发现】
数最多可以连出几条线段时,先选中一个点,有规律地向其他点连线,并注意数线段时不重复、不遗漏。
【问题探究】
2. 数一数下面图形中各有几个角。

按照上面的画法,如果图形中有8条射线,一共有几个角?
【分析探究】
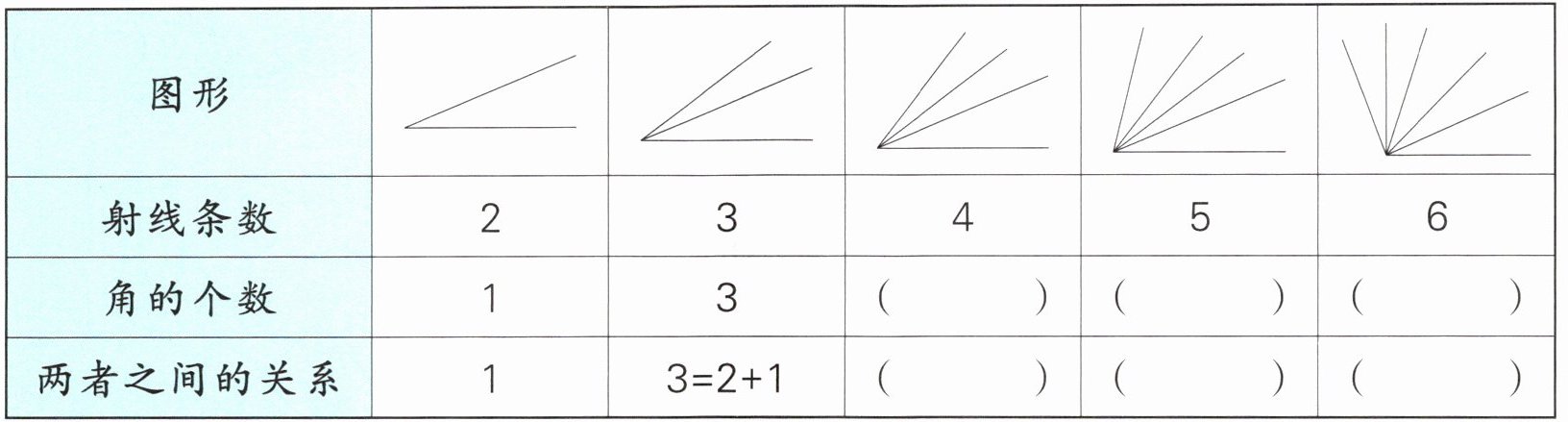
数角的个数时,关键在于找到角的个数与()条数之间的关系。
【规范解答】
【探索发现】
探究角的个数与射线条数之间的关系时,发现:从一个顶点引出n条射线,这n条射线组成的角的个数为$(n-1)+(n-2)+·s +3+2+1$。($n>1$)
【迁移运用】
1. 6个点最多可以连出()条线段,你的计算方式是什么?
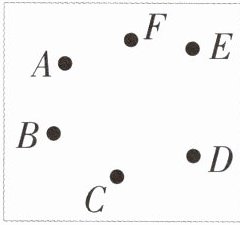
2. 数一数,图中一共有()个角,锐角有()个,直角有()个,钝角有()个。
3. 图中一共有多少条线段?多少个直角?
第五单元探究性作业 数线段和角
本单元我们已经学习了线和角,我们知道:2个点最多可以连出1条线段,那么3个点,4个点……最多可以连出多少条线段呢?让我们一起探究一下吧!
【问题探究】
1. 下图中的2个点、3个点、4个点、5个点……分别最多可以连出几条线段?

【分析探究】
方法1 选中一个点,向其他点分别连线。

方法2 依次连线,不连重复的。

【规范解答】
【探索发现】
数最多可以连出几条线段时,先选中一个点,有规律地向其他点连线,并注意数线段时不重复、不遗漏。
【问题探究】
2. 数一数下面图形中各有几个角。

按照上面的画法,如果图形中有8条射线,一共有几个角?
【分析探究】

数角的个数时,关键在于找到角的个数与()条数之间的关系。
【规范解答】
【探索发现】
探究角的个数与射线条数之间的关系时,发现:从一个顶点引出n条射线,这n条射线组成的角的个数为$(n-1)+(n-2)+·s +3+2+1$。($n>1$)
【迁移运用】
1. 6个点最多可以连出()条线段,你的计算方式是什么?

2. 数一数,图中一共有()个角,锐角有()个,直角有()个,钝角有()个。
3. 图中一共有多少条线段?多少个直角?
答案:
1.【分析探究】方法1: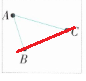 。 3
。 3
A C 2 A B 2
方法2: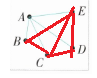 。 10
。 10
C、D、E 3 D、E 2 E 1
3 2 1 10
【规范解答】2个点最多可以连出1条线段;3个点最多可以连出3条线段;4个点最多可以连出6条线段;5个点最多可以连出10条线段。
2.【分析探究】(竖排)
6 6=1+2+3
10 10=1+2+3+4
15 15=1+2+3+4+5 射线
【规范解答】
6 10 15
7+6+5+4+3+2+1=28(个)
答:一共有28个角。
【迁移运用】
1.15
方法1:6×(6-1)=30(条)
30÷2=15(条)
2.10 5 2 3
3.13条线段 10个直角
1.【分析探究】方法1:
 。 3
。 3 A C 2 A B 2
方法2:
 。 10
。 10 C、D、E 3 D、E 2 E 1
3 2 1 10
【规范解答】2个点最多可以连出1条线段;3个点最多可以连出3条线段;4个点最多可以连出6条线段;5个点最多可以连出10条线段。
2.【分析探究】(竖排)
6 6=1+2+3
10 10=1+2+3+4
15 15=1+2+3+4+5 射线
【规范解答】
6 10 15
7+6+5+4+3+2+1=28(个)
答:一共有28个角。
【迁移运用】
1.15
方法1:6×(6-1)=30(条)
30÷2=15(条)
2.10 5 2 3
3.13条线段 10个直角
【迁移运用】

1. 6个点最多可以连出()条线段,你的计算方式是什么?
2. 数一数,图中一共有()个角,锐角有()个,直角有()个,钝角有()个。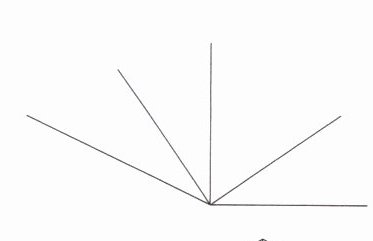
3. 图中一共有多少条线段?多少个直角?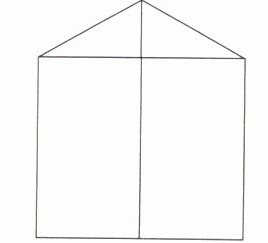

1. 6个点最多可以连出()条线段,你的计算方式是什么?
2. 数一数,图中一共有()个角,锐角有()个,直角有()个,钝角有()个。

3. 图中一共有多少条线段?多少个直角?

答案:
【迁移运用】
1.15
方法1:6×(6-1)=30(条)
30÷2=15(条)
2.10 5 2 3
3.13条线段 10个直角
1.15
方法1:6×(6-1)=30(条)
30÷2=15(条)
2.10 5 2 3
3.13条线段 10个直角
查看更多完整答案,请扫码查看


