8. 我们把分子为1的分数叫作单位分数.如$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,任何一个单位分数都可以拆分成两个不同单位分数的和,如$\frac{1}{2}= \frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}= \frac{1}{4}+\frac{1}{12}$,$\frac{1}{4}= \frac{1}{5}+\frac{1}{20}$,….
(1)根据对上述式子的观察,你会发现$\frac{1}{5}= \frac{1}{□}+\frac{1}{○}$,则□所表示的数为
(2)进一步思考,单位分数$\frac{1}{n}= \frac{1}{△}+\frac{1}{☆}$(n是不小于2的自然数),则△所表示的式子为
(1)根据对上述式子的观察,你会发现$\frac{1}{5}= \frac{1}{□}+\frac{1}{○}$,则□所表示的数为
6
,○所表示的数为30
;(2)进一步思考,单位分数$\frac{1}{n}= \frac{1}{△}+\frac{1}{☆}$(n是不小于2的自然数),则△所表示的式子为
$n+1$
,☆所表示的式子为$n(n+1)$
.
答案:
(1)6;30
(2)$n+1$;$n(n+1)$
(1)6;30
(2)$n+1$;$n(n+1)$
9. 新考向 传统文化 《礼记·杂记上》记载:“苇席以为屋,蒲席以为裳帷.”蒲为多年生草本植物,生池沼中,高近2米,根茎长在泥里,可食.其中涉及的自然数2属于(
A.计数
B.测量
C.标号
D.排序
B
)A.计数
B.测量
C.标号
D.排序
答案:
B
10. [2023·金华义乌月考]按一定规律排列的一列数依次为:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{10}$,$\frac{1}{15}$,$\frac{1}{26}$,$\frac{1}{35}$,…,按此规律排列下去,这列数中的第9个数是______
$\frac{1}{82}$
.
答案:
$\frac{1}{82}$
11. 如图,某旅行社推出了“西湖风景区一日游”的两种价格方案.
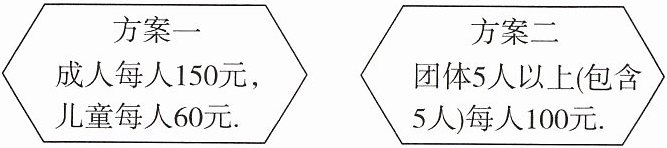
(1)5名成人,5名儿童,选择哪种方案合算?
(2)5名成人,10名儿童,怎样购票合算?

(1)5名成人,5名儿童,选择哪种方案合算?
(2)5名成人,10名儿童,怎样购票合算?
答案:
【解】
(1)方案一:$5× 150+5× 60=1\ 050$(元),方案二:$(5+5)× 100=1\ 000$(元),$1\ 050>1\ 000$,因此选择方案二合算.
(2)5名成人选方案二,10名儿童选方案一购票合算.
(1)方案一:$5× 150+5× 60=1\ 050$(元),方案二:$(5+5)× 100=1\ 000$(元),$1\ 050>1\ 000$,因此选择方案二合算.
(2)5名成人选方案二,10名儿童选方案一购票合算.
12. 母题 教材P8作业题T1 读完下面这段话,回答问题:
我们的教室长12 m,宽8 m,讲台长1.2 m,宽0.8 m,我们班有50人,占全年级人数的8%,多数同学都是13岁.
(1)在老师刚才描述中出现了哪些数?其中哪些属于计数?哪些属于测量?哪些属于标号或排序?
(2)你能将这些数进行分类吗?
(3)在实际生活中仅有整数和分数够用吗?请你举例说明.
我们的教室长12 m,宽8 m,讲台长1.2 m,宽0.8 m,我们班有50人,占全年级人数的8%,多数同学都是13岁.
(1)在老师刚才描述中出现了哪些数?其中哪些属于计数?哪些属于测量?哪些属于标号或排序?
(2)你能将这些数进行分类吗?
(3)在实际生活中仅有整数和分数够用吗?请你举例说明.
答案:
【解】
(1)在老师刚才描述中出现了:12、8、1.2、0.8、50、8%、13,其中属于计数的有50、8%、13,属于测量的有12、8、1.2、0.8,出现的数均不属于标号或排序;
(2)能.按整数和分数分类:整数有12、8、50、13,分数有1.2、0.8、8%;
(3)仅有整数和分数不够用,例如求圆的周长和面积时,发现圆周率,但圆周率的值并不能由两个整数相除而得;又如求边长为1的正方形对角线长时,求得的既不是整数也不是分数.(举例不唯一)
(1)在老师刚才描述中出现了:12、8、1.2、0.8、50、8%、13,其中属于计数的有50、8%、13,属于测量的有12、8、1.2、0.8,出现的数均不属于标号或排序;
(2)能.按整数和分数分类:整数有12、8、50、13,分数有1.2、0.8、8%;
(3)仅有整数和分数不够用,例如求圆的周长和面积时,发现圆周率,但圆周率的值并不能由两个整数相除而得;又如求边长为1的正方形对角线长时,求得的既不是整数也不是分数.(举例不唯一)
13. 新考法 阅读类比法 阅读材料:把无限循环小数化为分数,可以按如下方法进行:
以$0.\dot{3}$为例,令$0.\dot{3}= x$,
由$0.\dot{3}= 0.333…$,可知$10x= 3.333…$,所以$10x= 3+x$,解得$x= \frac{1}{3}$,于是$0.\dot{3}= \frac{1}{3}$.
(1)请把无限循环小数$0.\dot{7}$化为分数是
(2)请把无限循环小数$0.\dot{7}\dot{5}$化为分数;
(3)将$0.\dot{2}1\dot{6}与0.\dot{5}$的积化为小数,则小数点后第999位数字是
以$0.\dot{3}$为例,令$0.\dot{3}= x$,
由$0.\dot{3}= 0.333…$,可知$10x= 3.333…$,所以$10x= 3+x$,解得$x= \frac{1}{3}$,于是$0.\dot{3}= \frac{1}{3}$.
(1)请把无限循环小数$0.\dot{7}$化为分数是
$\frac{7}{9}$
;(2)请把无限循环小数$0.\dot{7}\dot{5}$化为分数;
【解】令$0.\dot{7}\dot{5}=x$,则$100x=75.757\ 5\cdots$,所以$100x=75+x$,所以$x=\frac{25}{33}$.
(3)将$0.\dot{2}1\dot{6}与0.\dot{5}$的积化为小数,则小数点后第999位数字是
0
.
答案:
(1)$\frac{7}{9}$
(2)【解】令$0.\dot{7}\dot{5}=x$,则$100x=75.757\ 5\cdots$,所以$100x=75+x$,所以$x=\frac{25}{33}$.
(3)0【点拨】令$0.\dot{2}1\dot{6}=x$,则$1\ 000x=216.216\ 216\cdots$,所以$1\ 000x=216+x$,所以$x=\frac{8}{37}$.令$0.\dot{5}=y$,则$10y=5.555\cdots$,所以$10y=5+y$,所以$y=\frac{5}{9}$,所以$\frac{8}{37}× \frac{5}{9}=\frac{40}{333}=0.120\ 120\cdots$.因为$999÷ 3=333$,所以小数点后第999位数字是0.
(1)$\frac{7}{9}$
(2)【解】令$0.\dot{7}\dot{5}=x$,则$100x=75.757\ 5\cdots$,所以$100x=75+x$,所以$x=\frac{25}{33}$.
(3)0【点拨】令$0.\dot{2}1\dot{6}=x$,则$1\ 000x=216.216\ 216\cdots$,所以$1\ 000x=216+x$,所以$x=\frac{8}{37}$.令$0.\dot{5}=y$,则$10y=5.555\cdots$,所以$10y=5+y$,所以$y=\frac{5}{9}$,所以$\frac{8}{37}× \frac{5}{9}=\frac{40}{333}=0.120\ 120\cdots$.因为$999÷ 3=333$,所以小数点后第999位数字是0.
查看更多完整答案,请扫码查看


