《2025年暑假生活指导山东教育出版社四年级语数综合》

5. 走进动物园

(1)把它们的体重按照从重到轻的顺序排列起来。
(2)大象的体重是袋鼠的多少倍？

答案： 【解析】：
(1) 首先将所有动物的体重单位统一为千克：
大象：4.8吨 = 4800千克
长颈鹿：0.88吨 = 880千克
按照体重从重到轻排列：
大象（4800千克） ＞ 长颈鹿（880千克） ＞ 袋鼠（80千克） ＞ 狼（50千克）
(2) 计算大象体重是袋鼠体重的多少倍：
大象体重 ÷ 袋鼠体重 = 4800千克 ÷ 80千克 = 60
【答案】：
(1) 4.8吨＞0.88吨＞80千克＞50千克
(2) 60

6. 超市大促销
洗发水
买一瓶30元,
买五瓶赠一瓶,
买八瓶赠两瓶。
(1)妈妈和同事们合伙买20瓶,怎样买合算？
(2)李阿姨有150元,最多能买几瓶洗发水？

答案： 【解析】：
(1) 对于第一个问题，我们需要考虑最优惠的购买方式。根据题目信息，买五瓶赠一瓶，买八瓶赠两瓶。我们需要找出购买20瓶洗发水的最优方案。
方案一：直接购买20瓶不享受任何赠送，需花费 20 × 30 = 600 元。
方案二：利用买五瓶赠一瓶的优惠，购买16瓶洗发水会赠送3瓶（因为16/5=3...1，即3组赠1瓶），还需单独购买1瓶才能达到20瓶，共需购买17瓶，花费 17 × 30 = 510 元。
方案三：利用买八瓶赠两瓶的优惠，购买16瓶洗发水会赠送4瓶（因为16/8=2，即2组赠2瓶），正好达到20瓶，花费 16 × 30 = 480 元。
比较三种方案，方案三最合算。
(2) 对于第二个问题，李阿姨有150元，我们需要计算她最多能买多少瓶洗发水。
如果直接购买，150元可以购买 150 / 30 = 5 瓶。
但如果我们考虑优惠，买五瓶可以赠送一瓶，所以实际上用150元可以买到 5 + 1 = 6 瓶。
我们还需要考虑是否能通过多次购买来获得更多优惠。然而，由于150元的限制，无法购买到8瓶以获得买八赠二的优惠。
因此，最多能买6瓶洗发水。
【答案】：
(1) 买16瓶赠送4瓶最合算。
(2) 最多能买6瓶洗发水。

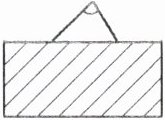
下面的三角形,只露出了一个角,这个三角形可能是什么三角形？你是怎么想的？

答案： 【解析】：
从图中可以看到，三角形只露出了一个锐角。
三角形的内角和总是$180^\circ$，且三角形的类型由它的内角决定。
只露出一个锐角，意味着其他两个角的情况未知。
如果其他两个角都是锐角，那么这个三角形就是锐角三角形。
如果其他两个角中有一个是直角，那么这个三角形就是直角三角形。
如果其他两个角中有一个是钝角（大于$90^\circ$的角），那么这个三角形就是钝角三角形。
由于只知道一个角是锐角，所以无法确定其他两个角的具体情况，因此这个三角形可能是锐角三角形、直角三角形或钝角三角形中的任何一种。
【答案】：锐角三角形、直角三角形或钝角三角形

在上面的三角形中,∠C是30°,沿着虚线剪去这个角后的图形是( )形,这个图形的内角和是( )。

答案： 【解析】：
本题考察的是图形的变换以及多边形内角和的概念。
首先，我们需要明确题目中的操作：沿着虚线剪去三角形中的一个角，即∠C，其度数为30°。
当我们沿着虚线剪去三角形的一个角后，新的图形将由原有的两个边和剪去角的虚线（即新的边）共同构成。这样，新的图形将是一个四边形，因为它由四条边围成。
接下来，我们需要确定这个四边形的内角和。根据多边形的性质，一个n边形的内角和可以通过公式(n-2)×180°来计算。对于四边形，n=4，所以内角和为(4-2)×180°=360°。
【答案】：
四边；360°