4. 激烈的比赛
在第32届奥运会女子铅球决赛中,中国运动员获得一枚金牌,这是中国田径队在第32届奥运会上的首金。
第32届奥运会女子铅球前三名成绩表:
运动员 成绩/米
中国运动员 20.58
美国运动员 19.79
新西兰运动员 19.62
(1)我国运动员成绩领先美国运动员多少米?
(2)新西兰运动员与我国运动员成绩相差多少米?
在第32届奥运会女子铅球决赛中,中国运动员获得一枚金牌,这是中国田径队在第32届奥运会上的首金。
第32届奥运会女子铅球前三名成绩表:
运动员 成绩/米
中国运动员 20.58
美国运动员 19.79
新西兰运动员 19.62
(1)我国运动员成绩领先美国运动员多少米?
(2)新西兰运动员与我国运动员成绩相差多少米?
答案:
【解析】:
(1) 我国运动员的成绩是20.58米,美国运动员的成绩是19.79米。要求我国运动员成绩领先美国运动员的米数,只需要用我国运动员的成绩减去美国运动员的成绩,即$20.58 - 19.79 = 0.79$米。
(2) 新西兰运动员的成绩是19.62米,我国运动员的成绩是20.58米。要求新西兰运动员与我国运动员成绩相差的米数,只需要用我国运动员的成绩减去新西兰运动员的成绩,即$20.58 - 19.62 = 0.96$米。
【答案】:
(1) 0.79米
(2) 0.96米
(1) 我国运动员的成绩是20.58米,美国运动员的成绩是19.79米。要求我国运动员成绩领先美国运动员的米数,只需要用我国运动员的成绩减去美国运动员的成绩,即$20.58 - 19.79 = 0.79$米。
(2) 新西兰运动员的成绩是19.62米,我国运动员的成绩是20.58米。要求新西兰运动员与我国运动员成绩相差的米数,只需要用我国运动员的成绩减去新西兰运动员的成绩,即$20.58 - 19.62 = 0.96$米。
【答案】:
(1) 0.79米
(2) 0.96米
1. 在下面的四边形中,请你用直尺任意画出2~4条线段,把四边形分成多个三角形,使锐角三角形、直角三角形、钝角三角形至少各有一个。


答案:
【解析】:
假设该四边形为梯形,假设上底在左,下底在右,上底的两个端点按照逆时针顺序分别为A,B,下底的两个端点分别为D,C。
连接$AC$,$BD$交于点$O$,过$O$作$BC$的平行线交$CD$于点$E$,连接$BE$,
此时$\triangle BCE$为锐角三角形,$\triangle AOD$为直角三角形,$\triangle AOB$和$\triangle DEC$为钝角三角形。(该题答案不唯一)
【答案】:连接$AC$,$BD$交于点$O$,过$O$作$BC$的平行线交$CD$于点$E$,连接$BE$。(该题答案不唯一)
假设该四边形为梯形,假设上底在左,下底在右,上底的两个端点按照逆时针顺序分别为A,B,下底的两个端点分别为D,C。
连接$AC$,$BD$交于点$O$,过$O$作$BC$的平行线交$CD$于点$E$,连接$BE$,
此时$\triangle BCE$为锐角三角形,$\triangle AOD$为直角三角形,$\triangle AOB$和$\triangle DEC$为钝角三角形。(该题答案不唯一)
【答案】:连接$AC$,$BD$交于点$O$,过$O$作$BC$的平行线交$CD$于点$E$,连接$BE$。(该题答案不唯一)
2. 下面有6根小棒,选取合适的3根,你能摆出几种三角形?画出简单的示意图。

能摆出( )种三角形。

能摆出( )种三角形。
答案:
【解析】:首先明确三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边。题目中给出的小棒长度分别为:3cm、3cm、5cm、5cm、5cm、6cm。
接下来,我们依次列举所有可能的三根小棒组合,并判断是否能组成三角形:
1. 3cm,3cm,5cm
两边之和:3+3=6>5,3+5=8>3,3+5=8>3
两边之差:5-3=2<3,5-3=2<3,3-3=0<5
满足条件,能组成三角形(等腰三角形)。
2. 3cm,3cm,6cm
两边之和:3+3=6,不满足“任意两边之和大于第三边”(等于第三边时无法组成三角形)
不能组成三角形。
3. 3cm,3cm,5cm(重复组合,已考虑)。
4. 3cm,5cm,5cm
两边之和:3+5=8>5,5+5=10>3,3+5=8>5
两边之差:5-3=2<5,5-5=0<3,5-3=2<5
满足条件,能组成三角形(等腰三角形)。
5. 3cm,5cm,5cm(重复组合,已考虑)。
6. 3cm,5cm,6cm
两边之和:3+5=8>6,5+6=11>3,3+6=9>5
两边之差:6-5=1<3,6-3=3<5,5-3=2<6
满足条件,能组成三角形(普通三角形)。
7. 3cm,5cm,6cm(重复组合,已考虑)。
8. 5cm,5cm,5cm
两边之和:5+5=10>5,满足等边三角形条件
能组成三角形(等边三角形)。
9. 5cm,5cm,6cm
两边之和:5+5=10>6,5+6=11>5,5+6=11>5
两边之差:6-5=1<5,6-5=1<5,5-5=0<6
满足条件,能组成三角形(等腰三角形)。
10. 其他重复组合(如5cm,5cm,5cm、5cm,5cm,6cm等均已考虑,无新组合)。
综上,有效的组合为:(3,3,5)、(3,5,5)、(3,5,6)、(5,5,5)、(5,5,6),共5种不同的三角形。
【答案】:5
接下来,我们依次列举所有可能的三根小棒组合,并判断是否能组成三角形:
1. 3cm,3cm,5cm
两边之和:3+3=6>5,3+5=8>3,3+5=8>3
两边之差:5-3=2<3,5-3=2<3,3-3=0<5
满足条件,能组成三角形(等腰三角形)。
2. 3cm,3cm,6cm
两边之和:3+3=6,不满足“任意两边之和大于第三边”(等于第三边时无法组成三角形)
不能组成三角形。
3. 3cm,3cm,5cm(重复组合,已考虑)。
4. 3cm,5cm,5cm
两边之和:3+5=8>5,5+5=10>3,3+5=8>5
两边之差:5-3=2<5,5-5=0<3,5-3=2<5
满足条件,能组成三角形(等腰三角形)。
5. 3cm,5cm,5cm(重复组合,已考虑)。
6. 3cm,5cm,6cm
两边之和:3+5=8>6,5+6=11>3,3+6=9>5
两边之差:6-5=1<3,6-3=3<5,5-3=2<6
满足条件,能组成三角形(普通三角形)。
7. 3cm,5cm,6cm(重复组合,已考虑)。
8. 5cm,5cm,5cm
两边之和:5+5=10>5,满足等边三角形条件
能组成三角形(等边三角形)。
9. 5cm,5cm,6cm
两边之和:5+5=10>6,5+6=11>5,5+6=11>5
两边之差:6-5=1<5,6-5=1<5,5-5=0<6
满足条件,能组成三角形(等腰三角形)。
10. 其他重复组合(如5cm,5cm,5cm、5cm,5cm,6cm等均已考虑,无新组合)。
综上,有效的组合为:(3,3,5)、(3,5,5)、(3,5,6)、(5,5,5)、(5,5,6),共5种不同的三角形。
【答案】:5
先画一画,再算一算,你能发现什么规律?
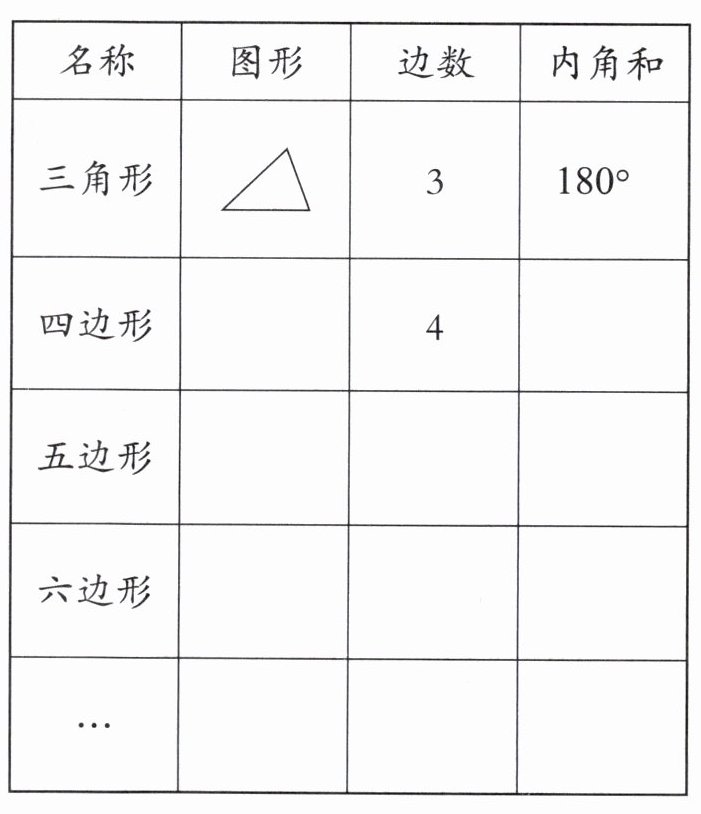

答案:
1. 首先画四边形、五边形、六边形(此处省略画图过程):
对于四边形:
连接四边形的一条对角线,可将四边形分成$2$个三角形。
因为三角形内角和是$180^{\circ}$,所以四边形内角和$=(4 - 2)×180^{\circ}=360^{\circ}$。
对于五边形:
从五边形的一个顶点出发,连接不相邻的顶点,可将五边形分成$3$个三角形。
所以五边形内角和$=(5 - 2)×180^{\circ}=540^{\circ}$。
对于六边形:
从六边形的一个顶点出发,连接不相邻的顶点,可将六边形分成$4$个三角形。
所以六边形内角和$=(6 - 2)×180^{\circ}=720^{\circ}$。
2. 然后找规律:
设多边形边数为$n$($n\geqslant3$且$n$为整数)。
从$n$边形的一个顶点出发,可引出$(n - 3)$条对角线,把$n$边形分成$(n - 2)$个三角形。
则$n$边形内角和公式为$(n - 2)×180^{\circ}$。
|名称|图形|边数|内角和|
|---|---|---|---|
|三角形|$\triangle$| $3$|$180^{\circ}$|
|四边形|$□$| $4$|$360^{\circ}$|
|五边形|\pentagon| $5$|$540^{\circ}$|
|六边形|\hexagon| $6$|$720^{\circ}$|
|...|...| $n$|$(n - 2)×180^{\circ}$|
所以四边形内角和$360^{\circ}$,五边形内角和$540^{\circ}$,六边形内角和$720^{\circ}$,规律是$n$边形内角和$(n - 2)×180^{\circ}$($n\geqslant3$且$n$为整数)。
对于四边形:
连接四边形的一条对角线,可将四边形分成$2$个三角形。
因为三角形内角和是$180^{\circ}$,所以四边形内角和$=(4 - 2)×180^{\circ}=360^{\circ}$。
对于五边形:
从五边形的一个顶点出发,连接不相邻的顶点,可将五边形分成$3$个三角形。
所以五边形内角和$=(5 - 2)×180^{\circ}=540^{\circ}$。
对于六边形:
从六边形的一个顶点出发,连接不相邻的顶点,可将六边形分成$4$个三角形。
所以六边形内角和$=(6 - 2)×180^{\circ}=720^{\circ}$。
2. 然后找规律:
设多边形边数为$n$($n\geqslant3$且$n$为整数)。
从$n$边形的一个顶点出发,可引出$(n - 3)$条对角线,把$n$边形分成$(n - 2)$个三角形。
则$n$边形内角和公式为$(n - 2)×180^{\circ}$。
|名称|图形|边数|内角和|
|---|---|---|---|
|三角形|$\triangle$| $3$|$180^{\circ}$|
|四边形|$□$| $4$|$360^{\circ}$|
|五边形|\pentagon| $5$|$540^{\circ}$|
|六边形|\hexagon| $6$|$720^{\circ}$|
|...|...| $n$|$(n - 2)×180^{\circ}$|
所以四边形内角和$360^{\circ}$,五边形内角和$540^{\circ}$,六边形内角和$720^{\circ}$,规律是$n$边形内角和$(n - 2)×180^{\circ}$($n\geqslant3$且$n$为整数)。
查看更多完整答案,请扫码查看


