《2025年暑假园地知识出版社四年级数学》

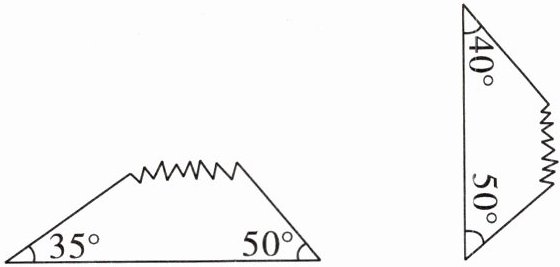
2. 下面是两块三角形的玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗？

第一个三角形原来是什么三角形：钝角三角形；第二个三角形原来是什么三角形：直角三角形

答案： $ 180^{\circ} - 35^{\circ} - 50^{\circ} = 95^{\circ} $ 钝角三角形
$ 180^{\circ} - 40^{\circ} - 50^{\circ} = 90^{\circ} $ 直角三角形

3. 一个直角三角形,其中一个锐角比另一个锐角多$10^{\circ }$,这两个锐角分别是多少度？

答案： $ 180^{\circ} - 90^{\circ} = 90^{\circ} $ $ (90^{\circ} - 10^{\circ}) \div 2 = 40^{\circ} $ $ 40^{\circ} + 10^{\circ} = 50^{\circ} $
这两个锐角分别是 $ 40^{\circ} $，$ 50^{\circ} $

4. 一个等腰三角形,其中一个角的度数是$70^{\circ }$,求另外两个角的度数。

答案： 若顶角为 $ 70^{\circ} $，则底角为 $ (180^{\circ} - 70^{\circ}) \div 2 = 55^{\circ} $
若底角为 $ 70^{\circ} $，则顶角为 $ 180^{\circ} - 70^{\circ} \times 2 = 40^{\circ} $
另外两个角的度数分别为 $ 55^{\circ} $，$ 55^{\circ} $
或 $ 70^{\circ} $，$ 40^{\circ} $。

5. 一个等腰三角形的一个底角与顶角的度数和是$125^{\circ }$,它的一个底角是多少度？顶角是多少度？

答案： 底角：$ 180^{\circ} - 125^{\circ} = 55^{\circ} $
顶角：$ 125^{\circ} - 55^{\circ} = 70^{\circ} $

6. 在一个三角形中,最大角是最小角的 3 倍,另一个角是最小角的 2 倍,求这个三角形的三个角的度数。

答案： 最小角：$ 180^{\circ} \div (3 + 2 + 1) = 30^{\circ} $
最大角：$ 30^{\circ} \times 3 = 90^{\circ} $
另一个角：$ 30^{\circ} \times 2 = 60^{\circ} $
三个角的度数分别为 $ 30^{\circ} $，$ 60^{\circ} $，$ 90^{\circ} $。