四、求角的度数。
1.(
1.(
54°
)(30°
)(35°
)(55°
)(60°
)
答案:
1. $ 54^{\circ} $ $ 30^{\circ} $ $ 35^{\circ} $ $ 55^{\circ} $ $ 60^{\circ} $
2. 如图,三角形$ABC$是等边三角形,已知$∠1= 35^{\circ }$,求$∠2$的度数。
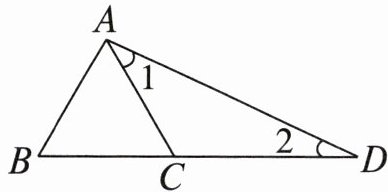
$∠2$的度数是

$∠2$的度数是
25°
。
答案:
2. $ \angle 2 = 60^{\circ} - 35^{\circ} = 25^{\circ} $
3. 如图,在大三角形$ABC$中,$∠1= 65^{\circ },∠2= 25^{\circ }$,求$∠4$的度数。
$∠3 = 180^{\circ} - 90^{\circ} - 25^{\circ} =$
$∠4 = 180^{\circ} - 65^{\circ} - 65^{\circ} =$
$∠3 = 180^{\circ} - 90^{\circ} - 25^{\circ} =$
$65^{\circ}$
$∠4 = 180^{\circ} - 65^{\circ} - 65^{\circ} =$
$50^{\circ}$
答案:
3. $ \angle 3 = 180^{\circ} - 90^{\circ} - 25^{\circ} = 65^{\circ} $
$ \angle 4 = 180^{\circ} - 65^{\circ} - 65^{\circ} = 50^{\circ} $
$ \angle 4 = 180^{\circ} - 65^{\circ} - 65^{\circ} = 50^{\circ} $
4. 如图,等边三角形内有一个等腰三角形,并且$∠1= ∠2,∠3= ∠4$,你能求出$∠5$的度数吗?
$∠5$的度数是
$∠5$的度数是
120°
。
答案:
4. $ \angle 1 = \angle 2 = 60^{\circ} ÷ 2 = 30^{\circ} $
$ \angle 3 = \angle 4 = 60^{\circ} ÷ 2 = 30^{\circ} $
$ \angle 5 = 180^{\circ} - 30^{\circ} - 30^{\circ} = 120^{\circ} $
$ \angle 3 = \angle 4 = 60^{\circ} ÷ 2 = 30^{\circ} $
$ \angle 5 = 180^{\circ} - 30^{\circ} - 30^{\circ} = 120^{\circ} $
1. 在一个直角三角形中,已知一个锐角是$35^{\circ }$,另一个锐角是多少度?
答案:
$ 180^{\circ} - 90^{\circ} - 35^{\circ} = 55^{\circ} $
查看更多完整答案,请扫码查看


