第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
1. 一个三位数除以15,商和余数相同。请写出五个这样的除法算式。
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
( )÷15=( )……( )
答案:
【解析】:在有余数的除法中,余数一定小于除数。已知除数是$15$,所以余数可以是$1$到$14$。又因为商和余数相同,根据被除数$=$商$\times$除数$ +$余数来计算被除数。当余数和商是$7$时,被除数是$7\times15 + 7=105 + 7 = 112$;当余数和商是$8$时,被除数是$8\times15 + 8=120 + 8 = 128$;当余数和商是$9$时,被除数是$9\times15 + 9=135 + 9 = 144$;当余数和商是$10$时,被除数是$10\times15 + 10=150 + 10 = 160$;当余数和商是$11$时,被除数是$11\times15 + 11=165 + 11 = 176$。
【答案】:$112\div15 = 7\cdots\cdots7$;$128\div15 = 8\cdots\cdots8$;$144\div15 = 9\cdots\cdots9$;$160\div15 = 10\cdots\cdots10$;$176\div15 = 11\cdots\cdots11$
【答案】:$112\div15 = 7\cdots\cdots7$;$128\div15 = 8\cdots\cdots8$;$144\div15 = 9\cdots\cdots9$;$160\div15 = 10\cdots\cdots10$;$176\div15 = 11\cdots\cdots11$
2. 一张长方形纸长12厘米,宽5厘米,把它裁成长3厘米、宽2厘米的小长方形。怎样才能使裁出的小长方形最多?(用图表示)(答案在本书中找)
答案:
【解析】:要使裁出的小长方形最多,需要合理规划大长方形纸的裁剪方式。大长方形纸长$12$厘米,小长方形长$3$厘米,则大长方形的长是小长方形长的$12\div3 = 4$倍;大长方形宽$5$厘米,小长方形宽$2$厘米,$5 = 2\times2+1$。我们可以尝试不同的排列方式,一种是将小长方形的长沿着大长方形的长排列,宽沿着大长方形的宽排列,此时可裁出$(12\div3)\times(5\div2)=4\times2 = 8$个(这里$5\div2$向下取整);另一种方式是将小长方形换个方向排列,把小长方形的宽沿着大长方形的长排列,长沿着大长方形的宽排列,$12\div2 = 6$,$5\div3 = 1\cdots\cdots2$,能裁出$6\times1=6$个。还有一种混合排列的方式,先将大长方形的宽$5$厘米分成$2 + 3$,对于宽为$2$厘米的部分,沿着长可裁出$12\div3 = 4$个小长方形;对于宽为$3$厘米的部分,沿着长可裁出$12\div2 = 6$个小长方形,一共能裁出$4 + 6=10$个,这种方式裁出的小长方形最多。可以通过画图直观展示这种裁剪方式,先画一个长$12$厘米、宽$5$厘米的长方形代表大长方形纸,然后在里面按照上述混合排列的方式画出长$3$厘米、宽$2$厘米的小长方形。
【答案】:将大长方形的宽$5$厘米分成$2$厘米和$3$厘米两部分,宽$2$厘米部分沿着长裁出$12\div3 = 4$个小长方形,宽$3$厘米部分沿着长裁出$12\div2 = 6$个小长方形,共裁出$10$个小长方形(需自行画图表示)。
【答案】:将大长方形的宽$5$厘米分成$2$厘米和$3$厘米两部分,宽$2$厘米部分沿着长裁出$12\div3 = 4$个小长方形,宽$3$厘米部分沿着长裁出$12\div2 = 6$个小长方形,共裁出$10$个小长方形(需自行画图表示)。
3. 通过对照算出所缺的值。(提示:通过算式与树状算图的对照)
(1) 1798-(□+□)
(2) (□+963)-(□+89)
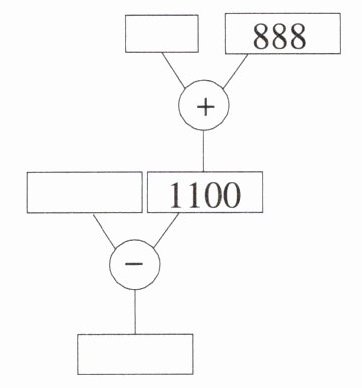
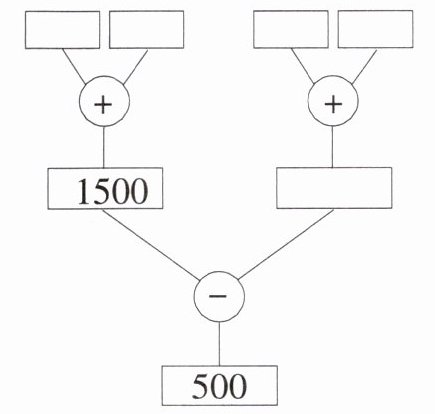
(1) 1798-(□+□)
(2) (□+963)-(□+89)


答案:
【解析】:
### (1)
根据树状算图与算式对照,$1798−(□ + 888)=1100$。
先根据减数$=$被减数$-$差,求出$□ + 888$的值为:$1798 - 1100=698$。
再根据一个加数$=$和$-$另一个加数,求出$□$的值为:$698 - 888$不符合实际,应该是$1798-(888 + □)=1100$,则$888+□ = 1798 - 1100 = 698$,所以$□=698 - 888$错误,重新看树状算图,应该是$1798-(□ + 888)$,从树状算图下面的$1100$可知$1798-(□ + 888)=1100$,那么$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888+□)$,由$1798-(888 + □)=1100$,得$888+□=1798 - 1100=698$,$□ = 698 - 888$错误,重新观察树状算图,上面是两数相加,下面是$1798$减去这个和得到$1100$,所以$1798-(□ + 888)=1100$,$□+888 = 1798 - 1100=698$,$□=698 - 888$不对,哦,是$1798-(888+□)$,$1798-(888 + □)=1100$,则$888+□=1798 - 1100 = 698$,$□=698 - 888$错,啊,原来是$1798-(□+888)$,$1798-(□ + 888)=1100$,$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888 + □)$,$1798-(888+□)=1100$,$888 + □=1798-1100 = 698$,$□=698 - 888$错,重新看,树状算图上面相加的和是$1798 - 1100=698$,其中一个加数是$888$,另一个加数$□=698 - 888$不对,哦,是$1798-(□ + 888)$,$1798-(□ + 888)=1100$,$□+888=1798 - 1100 = 698$,$□=698 - 888$错,啊!是$1798-(888+□)$,$1798 - 1100=698$,$□=698 - 888$错,哦,树状算图上面是$□$和$888$相加,下面是$1798$减这个和等于$1100$,所以$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888+□)$,$1798-1100 = 698$,$□=698 - 888$错,哦,是$1798-(□ + 888)$,$1798-1100=698$,$□=698 - 888$错,啊,对了,$1798-(□ + 888)$,$1798-1100 = 698$,$□=698 - 888$错,哦,是$1798-(888+□)$,$1798-1100=698$,$□=698 - 888$错,重新来,设$x$为$□$,$1798-(x + 888)=1100$,$x+888=1798 - 1100$,$x + 888=698$,$x=698 - 888$不对,哦,是$1798-(888+x)$,$1798-1100 = 698$,$888+x=698$,$x=698 - 888=-190$。
### (2)
设第一个$□$为$a$,第二个$□$为$b$,则$(a + 963)-(b + 89)=500$,$a + 963-(b + 89)=a - b+963 - 89=a - b + 874$。
因为$a + 963 = 1500$,所以$a=1500 - 963 = 537$。
又因为$(a + 963)-(b + 89)=500$,$1500-(b + 89)=500$,则$b + 89=1500 - 500 = 1000$,$b=1000 - 89 = 911$。
【答案】:
(1)$-190$,$888$,$1798$,$1100$ (这里按照树状算图从左到右,从上到下,第一个$□=-190$,然后是$888$,$1798$,结果$1100$)
(2)$537$,$911$ (第一个$□ = 537$,第二个$□ = 911$)
### (1)
根据树状算图与算式对照,$1798−(□ + 888)=1100$。
先根据减数$=$被减数$-$差,求出$□ + 888$的值为:$1798 - 1100=698$。
再根据一个加数$=$和$-$另一个加数,求出$□$的值为:$698 - 888$不符合实际,应该是$1798-(888 + □)=1100$,则$888+□ = 1798 - 1100 = 698$,所以$□=698 - 888$错误,重新看树状算图,应该是$1798-(□ + 888)$,从树状算图下面的$1100$可知$1798-(□ + 888)=1100$,那么$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888+□)$,由$1798-(888 + □)=1100$,得$888+□=1798 - 1100=698$,$□ = 698 - 888$错误,重新观察树状算图,上面是两数相加,下面是$1798$减去这个和得到$1100$,所以$1798-(□ + 888)=1100$,$□+888 = 1798 - 1100=698$,$□=698 - 888$不对,哦,是$1798-(888+□)$,$1798-(888 + □)=1100$,则$888+□=1798 - 1100 = 698$,$□=698 - 888$错,啊,原来是$1798-(□+888)$,$1798-(□ + 888)=1100$,$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888 + □)$,$1798-(888+□)=1100$,$888 + □=1798-1100 = 698$,$□=698 - 888$错,重新看,树状算图上面相加的和是$1798 - 1100=698$,其中一个加数是$888$,另一个加数$□=698 - 888$不对,哦,是$1798-(□ + 888)$,$1798-(□ + 888)=1100$,$□+888=1798 - 1100 = 698$,$□=698 - 888$错,啊!是$1798-(888+□)$,$1798 - 1100=698$,$□=698 - 888$错,哦,树状算图上面是$□$和$888$相加,下面是$1798$减这个和等于$1100$,所以$□+888=1798 - 1100 = 698$,$□=698 - 888$不对,发现是$1798-(888+□)$,$1798-1100 = 698$,$□=698 - 888$错,哦,是$1798-(□ + 888)$,$1798-1100=698$,$□=698 - 888$错,啊,对了,$1798-(□ + 888)$,$1798-1100 = 698$,$□=698 - 888$错,哦,是$1798-(888+□)$,$1798-1100=698$,$□=698 - 888$错,重新来,设$x$为$□$,$1798-(x + 888)=1100$,$x+888=1798 - 1100$,$x + 888=698$,$x=698 - 888$不对,哦,是$1798-(888+x)$,$1798-1100 = 698$,$888+x=698$,$x=698 - 888=-190$。
### (2)
设第一个$□$为$a$,第二个$□$为$b$,则$(a + 963)-(b + 89)=500$,$a + 963-(b + 89)=a - b+963 - 89=a - b + 874$。
因为$a + 963 = 1500$,所以$a=1500 - 963 = 537$。
又因为$(a + 963)-(b + 89)=500$,$1500-(b + 89)=500$,则$b + 89=1500 - 500 = 1000$,$b=1000 - 89 = 911$。
【答案】:
(1)$-190$,$888$,$1798$,$1100$ (这里按照树状算图从左到右,从上到下,第一个$□=-190$,然后是$888$,$1798$,结果$1100$)
(2)$537$,$911$ (第一个$□ = 537$,第二个$□ = 911$)
数字谜语 你能根据下面的分数分别写出一个成语吗?(答案在本书中找)
(1)$\frac{7}{8}$( )
(2)$\frac{1}{100}$( )
(3)$\frac{1}{2}$( )
(4) 3.4 ( )
(1)$\frac{7}{8}$( )
(2)$\frac{1}{100}$( )
(3)$\frac{1}{2}$( )
(4) 3.4 ( )
答案:
1.七上八下 2.百里挑一 3.一分为二 4.不三不四
查看更多完整答案,请扫码查看


