《2025年神龙牛皮卷海淀考王六年级数学下册人教版》

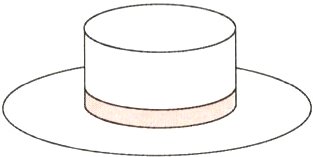
3. (北京东城区小升初)欣欣帽子厂设计的礼帽如图所示，帽顶部分是圆柱形，帽檐部分是一个圆环，其中帽顶的半径、高及帽檐的宽都是1 dm，做这样一顶帽子至少需要多少平方分米的布料? (6分)
　　

答案： 帽顶的面积:$3.14×1^{2}+2×3.14×1×1 = 9.42(dm^{2})$
帽檐的面积:$3.14×(1 + 1)^{2}-3.14×1^{2}=9.42(dm^{2})$
$9.42 + 9.42 = 18.84(dm^{2})$
答:做这样一顶帽子至少需要$18.84dm^{2}$的布料。

4. (北京平谷区小升初)有数据显示，每回收5吨废纸就能制造4吨新纸，相当于保护了85棵树木。某学校在开展垃圾分类两年以来共回收了7吨废纸，可以制造多少吨新纸? 相当于保护了多少棵树木? (用比例知识解答)(6分)

答案： 解:设可以制造 x 吨新纸，相当于保护了 y 棵树木。
$\frac{5}{4}=\frac{7}{x}$ $x = 5.6$
$\frac{85}{5}=\frac{y}{7}$ $y = 119$
答:可以制造 5.6 吨新纸，相当于保护了119 棵树木。

5. (北京丰台区小升初)某种牙膏的出口半径是3 mm，如果每天挤出2 cm的牙膏使用，那么这支牙膏能用80天。厂家为了促进牙膏的销量，将该牙膏的出口半径改成了4 mm，牙膏总量不变。乐乐每次挤出1.5 cm的牙膏使用，每天早晚刷牙一次，这支牙膏能用多少天? (6分)

答案： $2cm = 20mm$ $1.5cm = 15mm$
$3.14×3^{2}×20×80 = 45216(mm^{3})$
$3.14×4^{2}×15×2 = 1507.2(mm^{3})$
$45216÷1507.2 = 30$(天)
答:这支牙膏能用 30 天。

曼曼和欢欢分别以直角梯形的上底和下底所在的直线为轴，将直角梯形旋转一周，得到了两个立体图形。(10分)
　　　　
　(1)你同意谁的说法? 请把名字填在括号里。（ 　　　　）
　(2)甲、乙两个立体图形的体积比是（ 　　　　）。

答案：
(1)欢欢　
(2)$5:4$　[解析]观察甲、乙两个立体图形，都包含下半部分的小圆柱，下半部分的体积是相等的。甲的上半部分体积等于底面半径是 3 cm、高是$6 - 3 = 3(cm)$的圆柱体积的$\frac{2}{3}$，乙的上半部分体积等于底面半径是 3 cm、高是$6 - 3 = 3(cm)$的圆柱体积的$\frac{1}{3}$，所以甲、乙两个立体图形的体积不相等，且甲比乙的体积大，欢欢的说法正确。甲中大圆柱的高是 6 cm，圆锥的高是 3 cm，因此甲的体积是$3.14×3^{2}×6-\frac{1}{3}×3.14×3^{2}×3 = 141.3(cm^{3})$；乙中小圆柱的高是 3 cm，圆锥的高是 3 cm，因此乙的体积是$3.14×3^{2}×3+\frac{1}{3}×3.14×3^{2}×3 = 113.04(cm^{3})$，所以它们的体积比是$141.3:113.04 = 5:4$。