《2025年红对勾45分钟作业与单元评估九年级数学下册人教版》

1. 如图，在反比例函数$y = \frac{2}{x}(x＞0)$的图象上，有点$P_1$，$P_2$，$P_3$，$P_4$，它们的横坐标依次为1，2，3，4，分别过这些点作$x$轴与$y$轴的垂线，图中所构成的阴影部分的面积从左到右依次为$S_1$，$S_2$，$S_3$，则$S_1 + S_2 + S_3$等于 （ ）

A. 1
B. 1.5
C. 2
D. 无法确定

答案： B 解析：由题意可知点$P_1$，$P_2$，$P_3$，$P_4$的坐标分别为$(1,2)$，$(2,1)$，$(3,\frac{2}{3})$，$(4,\frac{1}{2})$。
∴由反比例函数的几何意义可知，$S_1 + S_2 + S_3 = 2 - 1\times\frac{1}{2}=\frac{3}{2}=1.5$。故选B。

2. 如图，已知矩形$ABCD$的对角线$BD$的中点$E$与点$B$都经过反比例函数$y = \frac{k}{x}(x＞0)$的图象，且$S_{矩形ABCD}=8$，则$k$的值为 （ ）

A. 2
B. 4
C. 6
D. 8

答案：
B 解析：如图
，过点E作$EM\perp AD$于点M，过点E作$EN\perp AB$于点N。设点$B(a,b)$。
∴$AB = a$。
∵$S_{矩形ABCD}=8$，
∴$AD=\frac{8}{a}$。
∵E为矩形ABCD的对角线BD的中点，$EM\perp AD$，$EN\perp AB$，
∴$ME// AB$，$EN// AD$。
∴$ME=\frac{1}{2}AB=\frac{a}{2}$，$EN=\frac{1}{2}AD=\frac{4}{a}$。
∴点$E(\frac{a}{2},b + \frac{4}{a})$。
∵点E与点B都经过反比例函数$y=\frac{k}{x}$的图象，
∴$\frac{a}{2}\cdot(b + \frac{4}{a}) = ab$。
∴$ab = 4$。由图可知，反比例函数$y=\frac{k}{x}$的图象经过点B，
∴$k = ab = 4$。故选B。

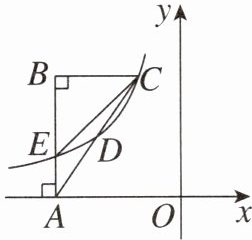
3. （2024重庆垫江县开学考试）反比例函数$y = \frac{k}{x}(x＜0)$的图象如图，在$\triangle ABC$中，$\angle B = 90^{\circ}$，边$BC\perp y$轴，边$AB\perp x$轴且与函数图象交于点$E$，边$AC$与此函数图象交于$C$，$D$两点，且$AE:BE = 1:2$，$S_{\triangle ACE}=2$，则$k$的值为_______.

答案： -6 解析：
∵$AE:BE = 1:2$，
∴$AE:AB = 1:3$。设点A的坐标为$(m,0)$，则点$E(m,\frac{k}{m})$，$B(m,\frac{3k}{m})$，$C(\frac{1}{3}m,\frac{3k}{m})$。
∴$AE=\frac{k}{m}$，$BC=\frac{1}{3}m - m = -\frac{2m}{3}$。
∵$S_{\triangle ACE}=2$，
∴$\frac{1}{2}AE\cdot BC = 2$。
∴$\frac{1}{2}\times\frac{k}{m}\times(-\frac{2m}{3}) = 2$。解得$k = - 6$。

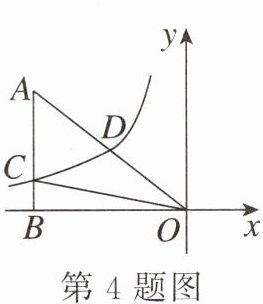
4. 如图，已知双曲线$y = \frac{k}{x}(x＜0)$经过$Rt\triangle OAB$的斜边$OA$的中点$D$，且与直角边$AB$相交于点$C$，连接$OC$. 若点$A$的坐标为$(-6,4)$，则$\triangle AOC$的面积为_______.

答案： 9 解析：
∵D为$Rt\triangle OAB$的斜边OA的中点，且点A的坐标为$(-6,4)$，
∴点D的坐标为$(-3,2)$。把点$(-3,2)$代入$y=\frac{k}{x}(x\lt0)$，得$k = - 6$。
∴双曲线的解析式为$y = -\frac{6}{x}$。
∵$AB\perp OB$，且点A的坐标为$(-6,4)$，
∴点C的横坐标为-6，代入解析式$y = -\frac{6}{x}$，得$y = 1$。
∴点C的坐标为$(-6,1)$。
∴$AC = 3$。又
∵$OB = 6$，
∴$S_{\triangle AOC}=\frac{1}{2}\times AC\times OB = 9$。

5. 如图，过点$O$作直线与双曲线$y = \frac{k}{x}(k\neq0)$交于$A$，$B$两点，过点$B$作$BC\perp x$轴于点$C$，作$BD\perp y$轴于点$D$. 在$x$轴、$y$轴上分别取点$E$，$F$，使点$A$，$E$，$F$在同一条直线上，且$AE = AF$. 设图中矩形$ODBC$的面积为$S_1$，$\triangle EOF$的面积为$S_2$，则$S_1$，$S_2$的数量关系是__________.

答案：
$2S_1 = S_2$ 解析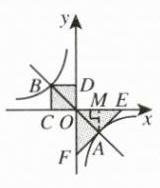：如图所示
，过点A作$AM\perp x$轴于点M。
∵$AM\perp x$轴，$BC\perp x$轴，$BD\perp y$轴，
∴$S_{矩形ODBC}=-k$，$S_{\triangle AOM}=\frac{1}{2}OM\cdot AM = -\frac{1}{2}k$。
∵$OF\perp x$轴，$AM\perp x$轴，
∴$OF// AM$。
∵$AE = AF$，
∴$AM=\frac{1}{2}OF$，$ME = OM=\frac{1}{2}OE$。
∴$S_{\triangle EOF}=\frac{1}{2}OE\cdot OF=\frac{1}{2}\times2OM\times2AM = 4S_{\triangle AOM}=-2k$。
∴$2S_{矩形ODBC}=S_{\triangle EOF}$，即$2S_1 = S_2$。

6. 如图，$A$，$B$两点在反比例函数$y = \frac{k}{x}(x＞0)$的图象上，其中$k＞0$，$AC\perp y$轴于点$C$，$BD\perp x$轴于点$D$，且$AC = 1$.
（1）若$k = 2$，则$AO$的长为__________，$\triangle BOD$的面积为________.
（2）若点$B$的横坐标为$k$，且$k＞1$，当$AO = AB$时，求$k$的值.

答案： 解：
(1)$\sqrt{5}$ 1
(2)
∵A，B两点在函数$y=\frac{k}{x}(x\gt0)$的图象上，$AC = 1$，
∴点$A(1,k)$，$B(k,1)$。
∴$AO=\sqrt{1^{2}+k^{2}}$，$AB=\sqrt{(k - 1)^{2}+(1 - k)^{2}}$。
∵$AO = AB$，
∴$\sqrt{1^{2}+k^{2}}=\sqrt{(k - 1)^{2}+(1 - k)^{2}}$。解得$k_1 = 2+\sqrt{3}$，$k_2 = 2-\sqrt{3}$。
∵$k\gt1$，
∴$k_1 = 2+\sqrt{3}$符合题意，$k_2 = 2-\sqrt{3}$不符合题意，舍去。
∴$k = 2+\sqrt{3}$。