《2025年红对勾45分钟作业与单元评估九年级数学下册人教版》

1. 如图，在平面直角坐标系中，直线$y=-x + 3$与$x$轴交于点$C$，与直线$AD$交于点$A(\frac{4}{3},\frac{5}{3})$，点$D$的坐标为$(0,1)$．
(1)直线$AD$的解析式为___________．
(2)直线$AD$与$x$轴交于点$B$，若$E$是直线$AD$上一动点(不与点$B$重合)，当$\triangle BOD$与$\triangle BCE$相似时，求点$E$的坐标.

答案：
解：\n（1）$y = \frac{1}{2}x + 1$\n（2）因为直线$AD$与$x$轴的交点$B$的坐标为$(-2,0)$，所以$OB = 2$。
因为点$D$的坐标为$(0,1)$，所以$OD = 1$。
所以$BD=\sqrt{OB^{2}+OD^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$。
因为直线$y = -x + 3$与$x$轴交于点$C(3,0)$，所以$OC = 3$，$BC = 2 + 3 = 5$。若$\triangle BOD$和$\triangle BCE$相似，分两种情况讨论：\n①如图，过点$C$作$CE\perp BA$交$BA$的延长线于点$E$，则$\triangle BOD\sim\triangle BEC$，所以$\frac{BD}{BC}=\frac{BO}{BE}=\frac{DO}{CE}$，即$\frac{\sqrt{5}}{5}=\frac{2}{BE}=\frac{1}{CE}$，解得$BE = 2\sqrt{5}$，$CE=\sqrt{5}$。
过点$E$作$EF\perp x$轴于点$F$，则$\frac{1}{2}BC\cdot EF=\frac{1}{2}BE\cdot CE$，所以$EF=\frac{BE\cdot CE}{BC}=\frac{2\sqrt{5}\times\sqrt{5}}{5}=2$，所以$\frac{1}{2}x + 1 = 2$，解得$x = 2$，所以点$E$的坐标为$(2,2)$。\n②
如图，过点$C$作$CE'\perp x$轴交直线$AD$于点$E'$，则$\triangle BOD\sim\triangle BCE'$，则$\frac{BO}{BC}=\frac{OD}{CE'}$，即$\frac{2}{5}=\frac{1}{CE'}$，解得$CE'=\frac{5}{2}$，所以点$E'$的坐标为$(3,\frac{5}{2})$。
综上所述，当$\triangle BOD$和$\triangle BCE$相似时，点$E$的坐标为$(2,2)$或$(3,\frac{5}{2})$。

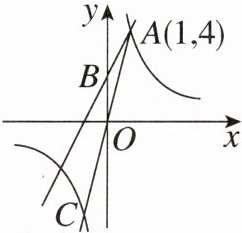
2. 如图，一次函数$y = 2x + b$与反比例函数$y=\frac{k}{x}(k\neq0)$的图象交于点$A(1,4)$，与$y$轴交于点$B$．
(1)$k =$______，$b =$______．
(2)连接并延长$AO$，与反比例函数$y=\frac{k}{x}(k\neq0)$的图象交于点$C$，点$D$在$y$轴上，若以点$O$，$C$，$D$为顶点的三角形与$\triangle AOB$相似，求点$D$的坐标.

答案： 解：\n（1）$4$ $2$\n（2）当点$D$落在$y$轴的正半轴上，则$\angle COD＞\angle ABO$，所以$\triangle COD$与$\triangle ABO$不可能相似。
当点$D$落在$y$轴的负半轴上，由（1），得一次函数的解析式为$y = 2x + 2$。当$x = 0$时，$y = 2$，所以点$B(0,2)$，所以$OB = 2$。因为点$A$，$C$在反比例函数的图象上，所以$CO = AO$。
若$\triangle COD\sim\triangle AOB$，则$\frac{CO}{AO}=\frac{DO}{BO}$，因为$CO = AO$，所以$BO = DO = 2$，所以点$D(0,-2)$。
若$\triangle COD\sim\triangle BOA$，则$\frac{OD}{OA}=\frac{OC}{OB}$，因为$OA = CO=\sqrt{17}$，$BO = 2$，所以$DO=\frac{17}{2}$，所以点$D(0,-\frac{17}{2})$。
综上所述，点$D$的坐标为$(0,-2)$或$(0,-\frac{17}{2})$。

3. (2024郑州期末)如图，反比例函数$y=\frac{k}{x}(x＞0)$的图象经过点$A(2,3)$，直线$l$经过点$A$和点$B(0,4)$，与$x$轴交于点$C$，直线$l$的解析式为$y = mx + n$．
(1)求反比例函数与一次函数的解析式.
(2)在$y$轴上是否存在一点$P$，使得以点$A$，$B$，$P$为顶点的三角形与$\triangle OBC$相似？若存在，请求出点$P$的坐标；若不存在，请说明理由.

答案：
解：\n（1）将点$A(2,3)$代入$y=\frac{k}{x}$中，得$k = 6$，所以反比例函数的解析式为$y=\frac{6}{x}$。
将点$A(2,3)$，$B(0,4)$代入$y = mx + n$中，得$\begin{cases}n = 4\\2m + n = 3\end{cases}$，解得$\begin{cases}m=-\frac{1}{2}\\n = 4\end{cases}$，所以一次函数的解析式为$y=-\frac{1}{2}x + 4$。\n（2）存在点$P$，使得以点$A$，$B$，$P$为顶点的三角形与$\triangle OBC$相似。
当$y = 0$时，$-\frac{1}{2}x + 4 = 0$，解得$x = 8$，所以点$C(8,0)$。
因为点$B(0,4)$，所以$OB = 4$，$OC = 8$，所以$\frac{OB}{OC}=\frac{1}{2}$。
因为$\triangle OBC$是直角三角形，所以$\triangle APB$也是直角三角形。\n如图1，当$\angle APB = 90^{\circ}$时，$\triangle OBC\sim\triangle PBA$，所以$\frac{OB}{PB}=\frac{OC}{PA}$，因为$\angle APB=\angle COB = 90^{\circ}$，所以$AP// OC$，$AP = 2$，所以$\frac{4}{PB}=\frac{8}{2}$，$PB = 1$，所以点$P(0,3)$。\n如图2，当$\angle PAB = 90^{\circ}$时，$\triangle OBC\sim\triangle ABP$，所以$\frac{OB}{AB}=\frac{BC}{BP}$。
由勾股定理，得$AB=\sqrt{(4 - 3)^{2}+2^{2}}=\sqrt{5}$，$BC=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$，所以$\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{BP}$，$BP = 5$，所以点$P(0,-1)$。
综上所述，$P$点的坐标为$(0,3)$或$(0,-1)$。