1.(2024迁安期末)如图,在Rt△ABC中,∠C = 90°,则sin A的值为( )

A. $\frac{a}{b}$
B. $\frac{a}{c}$
C. $\frac{b}{c}$
D. $\frac{b}{a}$

A. $\frac{a}{b}$
B. $\frac{a}{c}$
C. $\frac{b}{c}$
D. $\frac{b}{a}$
答案:
B 解析:在Rt△ABC中,∠C = 90°,则sin A = $\frac{a}{c}$。故选B。
2.(2024六安期末)正方形网格中,∠AOB如图放置,则sin∠AOB的值为( )
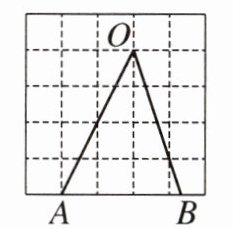
A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. 1
D. $\frac{\sqrt{3}}{3}$

A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. 1
D. $\frac{\sqrt{3}}{3}$
答案:
B 解析:如图,连接AD,CD,设正方形的网格边长是1,则根据勾股定理可以得到:
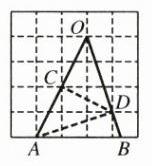
OD = AD = $\sqrt{10}$,OC = AC = $\sqrt{5}$,在△ODA中,由等腰三角形三线合一,得∠OCD = 90°,则CD = $\sqrt{OD^{2}-OC^{2}}$ = $\sqrt{5}$。
∴sin∠AOB = $\frac{CD}{OD}$ = $\frac{\sqrt{5}}{\sqrt{10}}$ = $\frac{\sqrt{2}}{2}$。故选B。
B 解析:如图,连接AD,CD,设正方形的网格边长是1,则根据勾股定理可以得到:

OD = AD = $\sqrt{10}$,OC = AC = $\sqrt{5}$,在△ODA中,由等腰三角形三线合一,得∠OCD = 90°,则CD = $\sqrt{OD^{2}-OC^{2}}$ = $\sqrt{5}$。
∴sin∠AOB = $\frac{CD}{OD}$ = $\frac{\sqrt{5}}{\sqrt{10}}$ = $\frac{\sqrt{2}}{2}$。故选B。
2. 如图,在4×4的正方形网格中,小正方形的顶点称为格点. 若△ABC的顶点都在格点上,则sin∠ABC的值是( )
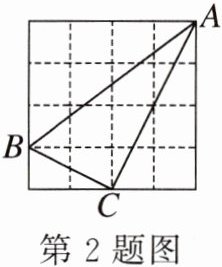
A. $\frac{1}{2}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{5}$
D. $\frac{1}{3}$

A. $\frac{1}{2}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{5}$
D. $\frac{1}{3}$
答案:
B 解析:由题意可知,AB = $\sqrt{3^{2}+4^{2}}$ = 5,AC = $\sqrt{2^{2}+4^{2}}$ = $2\sqrt{5}$,BC = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$。
∵AB² = 25,AC² = 20,BC² = 5,
∴AB² = AC² + BC²。
∴△ABC是直角三角形,∠ACB = 90°。
∴sin∠ABC = $\frac{AC}{AB}$ = $\frac{2\sqrt{5}}{5}$。
故选B。
∵AB² = 25,AC² = 20,BC² = 5,
∴AB² = AC² + BC²。
∴△ABC是直角三角形,∠ACB = 90°。
∴sin∠ABC = $\frac{AC}{AB}$ = $\frac{2\sqrt{5}}{5}$。
故选B。
3. 如图,在Rt△ABC中,∠C = 90°,∠B = α,∠ADC = β,用含α和β的代数式表示$\frac{AD}{AB}$的值为__________.


答案:
$\frac{\sin\alpha}{\sin\beta}$ 解析:在Rt△ABC中,sin α = $\frac{AC}{AB}$,
∴AB = $\frac{AC}{\sin\alpha}$。
在Rt△ADC中,sin β = $\frac{AC}{AD}$,
∴AD = $\frac{AC}{\sin\beta}$。
∴$\frac{AD}{AB}$ = $\frac{AC}{\sin\beta}$·$\frac{\sin\alpha}{AC}$ = $\frac{\sin\alpha}{\sin\beta}$。
∴AB = $\frac{AC}{\sin\alpha}$。
在Rt△ADC中,sin β = $\frac{AC}{AD}$,
∴AD = $\frac{AC}{\sin\beta}$。
∴$\frac{AD}{AB}$ = $\frac{AC}{\sin\beta}$·$\frac{\sin\alpha}{AC}$ = $\frac{\sin\alpha}{\sin\beta}$。
4.(推理能力)如图,AC是⊙O的直径,PA⊥AC,连接OP,弦CB//OP,直线PB交直线AC于点D,BD = 2PA.
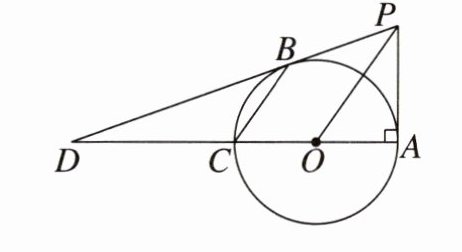
(1)求证:直线PB是⊙O的切线.
(2)探究线段PO与线段BC之间的数量关系,并加以证明.
(3)求sin∠OPA的值.

(1)求证:直线PB是⊙O的切线.
(2)探究线段PO与线段BC之间的数量关系,并加以证明.
(3)求sin∠OPA的值.
答案:
解:(1)证明:如图,连接OB。

∵PA⊥AC,
∴∠PAO = 90°。
∵BC//OP,
∴∠BCO = ∠POA,∠CBO = ∠POB。
∵OB = OC,
∴∠OBC = ∠OCB。
∴∠POB = ∠POA。
又
∵PO = PO,OB = OA,
∴△POB≌△POA(SAS)。
∴∠PBO = ∠PAO = 90°。
∵OB是⊙O的半径,
∴直线PB是⊙O的切线。
(2)2PO = 3BC。
证明:
∵△POB≌△POA,
∴PB = PA。
∵BD = 2PA,
∴BD = 2PB。
∴$\frac{BD}{PD}$ = $\frac{2}{3}$。
∵BC//PO,
∴△DBC∽△DPO。
∴$\frac{BC}{PO}$ = $\frac{BD}{PD}$ = $\frac{2}{3}$。
∴2PO = 3BC。
(3)
∵CB//OP,
∴△DBC∽△DPO。
∴$\frac{DC}{DO}$ = $\frac{BD}{PD}$ = $\frac{2}{3}$,即DC = $\frac{2}{3}$OD。
∵OC + CD = OD,
∴OC = $\frac{1}{3}$OD。
∴DC = 2OC。
设OA = x,PA = y。则OD = 3x,OB = x,BD = 2y。
在Rt△OBD中,由勾股定理,得OD² = OB² + BD²,$(3x)^{2}=x^{2}+(2y)^{2}$,即2x² = y²。
∵x>0,y>0,
∴y = $\sqrt{2}x$,OP = $\sqrt{x^{2}+y^{2}}$ = $\sqrt{3}x$。
∴sin∠OPA = $\frac{OA}{OP}$ = $\frac{x}{\sqrt{3}x}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$。
解:(1)证明:如图,连接OB。

∵PA⊥AC,
∴∠PAO = 90°。
∵BC//OP,
∴∠BCO = ∠POA,∠CBO = ∠POB。
∵OB = OC,
∴∠OBC = ∠OCB。
∴∠POB = ∠POA。
又
∵PO = PO,OB = OA,
∴△POB≌△POA(SAS)。
∴∠PBO = ∠PAO = 90°。
∵OB是⊙O的半径,
∴直线PB是⊙O的切线。
(2)2PO = 3BC。
证明:
∵△POB≌△POA,
∴PB = PA。
∵BD = 2PA,
∴BD = 2PB。
∴$\frac{BD}{PD}$ = $\frac{2}{3}$。
∵BC//PO,
∴△DBC∽△DPO。
∴$\frac{BC}{PO}$ = $\frac{BD}{PD}$ = $\frac{2}{3}$。
∴2PO = 3BC。
(3)
∵CB//OP,
∴△DBC∽△DPO。
∴$\frac{DC}{DO}$ = $\frac{BD}{PD}$ = $\frac{2}{3}$,即DC = $\frac{2}{3}$OD。
∵OC + CD = OD,
∴OC = $\frac{1}{3}$OD。
∴DC = 2OC。
设OA = x,PA = y。则OD = 3x,OB = x,BD = 2y。
在Rt△OBD中,由勾股定理,得OD² = OB² + BD²,$(3x)^{2}=x^{2}+(2y)^{2}$,即2x² = y²。
∵x>0,y>0,
∴y = $\sqrt{2}x$,OP = $\sqrt{x^{2}+y^{2}}$ = $\sqrt{3}x$。
∴sin∠OPA = $\frac{OA}{OP}$ = $\frac{x}{\sqrt{3}x}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$。
3. 如图,在△ACB中,∠C = 90°,sin B = $\frac{1}{2}$. 若AC = 6,则BC的长为( )
A. 8 B. 12 C. 6$\sqrt{3}$ D. 12$\sqrt{3}$

A. 8 B. 12 C. 6$\sqrt{3}$ D. 12$\sqrt{3}$
答案:
C 解析:在Rt△ACB中,sin B = $\frac{AC}{AB}$ = $\frac{6}{AB}$ = $\frac{1}{2}$,
∴AB = 12。
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{12^{2}-6^{2}}$ = $6\sqrt{3}$。
故选C。
∴AB = 12。
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{12^{2}-6^{2}}$ = $6\sqrt{3}$。
故选C。
4. 如图,$l_1// l_2$,A,B分别是直线$l_1$,$l_2$上的点,AB = 3,sin α = $\frac{2}{3}$,则直线$l_1$与$l_2$之间的距离为______.
答案:
2 解析:如图,过点A作AC⊥l₂于点C。

∵sin α = $\frac{AC}{AB}$,
∴AC = AB·sin α。
∵AB = 3,sin α = $\frac{2}{3}$,
∴AC = 3×$\frac{2}{3}$ = 2。
∴直线l₁与l₂之间的距离为2。
2 解析:如图,过点A作AC⊥l₂于点C。

∵sin α = $\frac{AC}{AB}$,
∴AC = AB·sin α。
∵AB = 3,sin α = $\frac{2}{3}$,
∴AC = 3×$\frac{2}{3}$ = 2。
∴直线l₁与l₂之间的距离为2。
1. 在△ABC中,已知∠C = 90°,AC = 4$\sqrt{5}$,sin A = $\frac{2}{3}$,那么BC边的长是( )
A. 2$\sqrt{5}$
B. 8
C. 4$\sqrt{5}$
D. 12
A. 2$\sqrt{5}$
B. 8
C. 4$\sqrt{5}$
D. 12
答案:
B 解析:
∵sin A = $\frac{2}{3}$ = $\frac{BC}{AB}$,
∴设BC = 2k,则AB = 3k。
由勾股定理,得AC² + BC² = AB²,
即$(4\sqrt{5})^{2}+(2k)^{2}=(3k)^{2}$。
解得k = 4(负值已舍去)。
∴BC = 2k = 8。
故选B。
∵sin A = $\frac{2}{3}$ = $\frac{BC}{AB}$,
∴设BC = 2k,则AB = 3k。
由勾股定理,得AC² + BC² = AB²,
即$(4\sqrt{5})^{2}+(2k)^{2}=(3k)^{2}$。
解得k = 4(负值已舍去)。
∴BC = 2k = 8。
故选B。
查看更多完整答案,请扫码查看


