1.(2024秦皇岛青龙县期末)如图,在△ABC中,点D,E分别在边AB,AC上,DE与BC不平行,添加下列条件之一仍不能判定△ADE∽△ACB的是( )

A. $\frac{AD}{AC}=\frac{AE}{AB}$
B. $\frac{AE}{AB}=\frac{DE}{BC}$
C. ∠AED = ∠B
D. ∠ADE = ∠C

A. $\frac{AD}{AC}=\frac{AE}{AB}$
B. $\frac{AE}{AB}=\frac{DE}{BC}$
C. ∠AED = ∠B
D. ∠ADE = ∠C
答案:
B
- **解析**:因为$\angle DAE=\angle CAB$,所以当$\angle ADE = \angle C$时,$\triangle ADE\sim\triangle ACB$;当$\angle AED=\angle B$时,$\triangle ADE\sim\triangle ACB$;当$\frac{AD}{AC}=\frac{AE}{AB}$时,$\triangle ADE\sim\triangle ACB$。故选B。
- **解析**:因为$\angle DAE=\angle CAB$,所以当$\angle ADE = \angle C$时,$\triangle ADE\sim\triangle ACB$;当$\angle AED=\angle B$时,$\triangle ADE\sim\triangle ACB$;当$\frac{AD}{AC}=\frac{AE}{AB}$时,$\triangle ADE\sim\triangle ACB$。故选B。
2. 如图,在菱形ABCD中,点E在边AD上,射线CE交BA的延长线于点F. 若$\frac{AE}{ED}=\frac{1}{2}$,AB = 3,则AF的长为( )

A. 1
B. $\frac{1}{2}$
C. $\frac{3}{2}$
D. 2

A. 1
B. $\frac{1}{2}$
C. $\frac{3}{2}$
D. 2
答案:
C
- **解析**:因为四边形$ABCD$为菱形,所以$AD// CB$,$AB = BC = AD$。
- 又因为$\frac{AE}{ED}=\frac{1}{2}$,所以$\frac{AE}{AD}=\frac{1}{3}$,进而$\frac{AE}{BC}=\frac{1}{3}$。
- 由于$AD// CB$,所以$\triangle FAE\sim\triangle FBC$,则$\frac{AF}{BF}=\frac{AE}{BC}=\frac{1}{3}$,即$\frac{AF}{AF + 3}=\frac{1}{3}$,解得$AF=\frac{3}{2}$。故选C。
- **解析**:因为四边形$ABCD$为菱形,所以$AD// CB$,$AB = BC = AD$。
- 又因为$\frac{AE}{ED}=\frac{1}{2}$,所以$\frac{AE}{AD}=\frac{1}{3}$,进而$\frac{AE}{BC}=\frac{1}{3}$。
- 由于$AD// CB$,所以$\triangle FAE\sim\triangle FBC$,则$\frac{AF}{BF}=\frac{AE}{BC}=\frac{1}{3}$,即$\frac{AF}{AF + 3}=\frac{1}{3}$,解得$AF=\frac{3}{2}$。故选C。
3. 如图,在△ABC中,点D,E分别在边AB,AC上,连接DE.
(1)若AD·AB = AE·AC,求证:△ADE∽△ACB.
(2)若AB = 8,AC = 6,AD = 3,当AE = ________时,△ADE与△ACB相似.

(1)若AD·AB = AE·AC,求证:△ADE∽△ACB.
(2)若AB = 8,AC = 6,AD = 3,当AE = ________时,△ADE与△ACB相似.

答案:
- **(1)证明**:因为$AD\cdot AB = AE\cdot AC$,所以$\frac{AD}{AC}=\frac{AE}{AB}$。
- 又因为$\angle A=\angle A$,所以$\triangle ADE\sim\triangle ACB$。
- **(2)**$\frac{9}{4}$或$4$
- 又因为$\angle A=\angle A$,所以$\triangle ADE\sim\triangle ACB$。
- **(2)**$\frac{9}{4}$或$4$
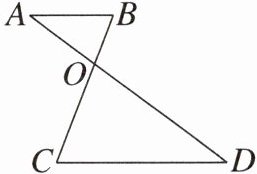
4. 如图,AD,BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( )
A. AB//CD
B. ∠A = ∠D
C. $\frac{OA}{OD}=\frac{OB}{OC}$
D. $\frac{OA}{OD}=\frac{AB}{CD}$

A. AB//CD
B. ∠A = ∠D
C. $\frac{OA}{OD}=\frac{OB}{OC}$
D. $\frac{OA}{OD}=\frac{AB}{CD}$
答案:
D
- **解析**:A. 由$AB// CD$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- B. 由$\angle AOB=\angle DOC$,$\angle A=\angle D$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- C. 由$\frac{OA}{OD}=\frac{OB}{OC}$,$\angle AOB=\angle DOC$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- D. 已知两组对应边的比相等,但其夹角不一定对应相等,不能判定$\triangle AOB$与$\triangle DOC$相似,故本选项符合题意。故选D。
- **解析**:A. 由$AB// CD$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- B. 由$\angle AOB=\angle DOC$,$\angle A=\angle D$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- C. 由$\frac{OA}{OD}=\frac{OB}{OC}$,$\angle AOB=\angle DOC$能判定$\triangle AOB\sim\triangle DOC$,故本选项不符合题意。
- D. 已知两组对应边的比相等,但其夹角不一定对应相等,不能判定$\triangle AOB$与$\triangle DOC$相似,故本选项符合题意。故选D。
5. 如图,BE是△ABC的角平分线,延长BE至点D,使得BC = CD.
求证:△AEB∽△CED.

求证:△AEB∽△CED.

答案:
**证明**:因为$BE$是$\triangle ABC$的角平分线,所以$\angle ABE=\angle CBE$。
- 因为$BC = CD$,所以$\angle CDE=\angle CBE=\angle ABE$。
- 又因为$\angle AEB=\angle CED$,所以$\triangle AEB\sim\triangle CED$。
- 因为$BC = CD$,所以$\angle CDE=\angle CBE=\angle ABE$。
- 又因为$\angle AEB=\angle CED$,所以$\triangle AEB\sim\triangle CED$。
6.(2024西安长安区期末)如图,已知∠1 = ∠2,点D在BC上,添加下列条件后,仍无法判定△ABC∽△ADE的是( )

A. ∠B = ∠ADE
B. ∠2 = ∠EDC
C. $\frac{AB}{AC}=\frac{AD}{AE}$
D. $\frac{AB}{AD}=\frac{BC}{DE}$

A. ∠B = ∠ADE
B. ∠2 = ∠EDC
C. $\frac{AB}{AC}=\frac{AD}{AE}$
D. $\frac{AB}{AD}=\frac{BC}{DE}$
答案:
D
- **解析**:A. 因为$\angle1=\angle2$,所以$\angle1+\angle DAC=\angle2+\angle DAC$,即$\angle BAC=\angle DAE$。又因为$\angle B=\angle ADE$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- B. 因为$\angle2=\angle EDC$,所以$\angle E=\angle C$。又因为$\angle BAC=\angle DAE$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- C. 因为$\angle BAC=\angle DAE$,$\frac{AB}{AC}=\frac{AD}{AE}$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- D. $\angle BAC=\angle DAE$,$\frac{AB}{AD}=\frac{BC}{DE}$,不符合相似三角形的判定定理,不能推出$\triangle ABC\sim\triangle ADE$,故本选项符合题意。故选D。
- **解析**:A. 因为$\angle1=\angle2$,所以$\angle1+\angle DAC=\angle2+\angle DAC$,即$\angle BAC=\angle DAE$。又因为$\angle B=\angle ADE$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- B. 因为$\angle2=\angle EDC$,所以$\angle E=\angle C$。又因为$\angle BAC=\angle DAE$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- C. 因为$\angle BAC=\angle DAE$,$\frac{AB}{AC}=\frac{AD}{AE}$,所以$\triangle ABC\sim\triangle ADE$。故本选项不符合题意。
- D. $\angle BAC=\angle DAE$,$\frac{AB}{AD}=\frac{BC}{DE}$,不符合相似三角形的判定定理,不能推出$\triangle ABC\sim\triangle ADE$,故本选项符合题意。故选D。
7. 如图,在Rt△ABC中,∠ACB = 90°,∠B = 30°,将△ABC绕点C按顺时针方向旋转n°后,得到△DEC,点D刚好落在边AB上,DE交BC于点O.
(1)n的值是________.
(2)若F是DE的中点,求证:△ABC∽△FCO.

(1)n的值是________.
(2)若F是DE的中点,求证:△ABC∽△FCO.

答案:
- **(1)**$60$
- **(2)证明**:因为$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,所以$\angle A=90^{\circ}-\angle B = 60^{\circ}$。
- 由旋转,得$CD = CA$,所以$\triangle ACD$是等边三角形,$\angle ACD = 60^{\circ}$。
- 因为$\triangle ABC$绕点$C$旋转后得$\triangle DEC$,所以$\angle CDE=\angle A = 60^{\circ}$,$\angle DCE=\angle ACB = 90^{\circ}$,所以$\angle CDE=\angle ACD$,$AC// DE$,$\angle COF=\angle ACB = 90^{\circ}$。
- 在$Rt\triangle DCE$中,因为$F$是$DE$的中点,所以$CF = DF$,$\triangle CDF$为等边三角形,$\angle DFC = 60^{\circ}$,$\angle A=\angle OFC$,所以$\triangle ABC\sim\triangle FCO$。
- **(2)证明**:因为$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,所以$\angle A=90^{\circ}-\angle B = 60^{\circ}$。
- 由旋转,得$CD = CA$,所以$\triangle ACD$是等边三角形,$\angle ACD = 60^{\circ}$。
- 因为$\triangle ABC$绕点$C$旋转后得$\triangle DEC$,所以$\angle CDE=\angle A = 60^{\circ}$,$\angle DCE=\angle ACB = 90^{\circ}$,所以$\angle CDE=\angle ACD$,$AC// DE$,$\angle COF=\angle ACB = 90^{\circ}$。
- 在$Rt\triangle DCE$中,因为$F$是$DE$的中点,所以$CF = DF$,$\triangle CDF$为等边三角形,$\angle DFC = 60^{\circ}$,$\angle A=\angle OFC$,所以$\triangle ABC\sim\triangle FCO$。
查看更多完整答案,请扫码查看


