第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 直接写出得数。
7.8÷6 = 4.2÷1.4 = 3.9×200 = 2×3.14×10 =
20² - 9² = 0.25 + 0.75 = 1.2 - 0.8 = 3.42 - 0.5 - 1.5 =
5.8 + 2.35 = 1.5×80 = 0.77÷11 = 12.56÷3.14÷2 =
8.47 - 2.39 = 5 - 0.08 = 3.25 - 1.2 = 0.5÷0.05×0.2 =
0.2×4.9 = 5.3÷0.1 = 1.58 + 5.2 = 3.14×6²÷4 =
9.5÷5 = 1.85×20 = 0.88 + 2.2 = 2÷0.25×3.14 =
0.14×5 = 5.9 - 5.59 = 40×3.14 = 19.8 - 6×0.8 =
6 - 1.35 = 3.7 + 17.3 = 2.7×4 = 13.68 - 3.14 - 3.14 =
7.8÷6 = 4.2÷1.4 = 3.9×200 = 2×3.14×10 =
20² - 9² = 0.25 + 0.75 = 1.2 - 0.8 = 3.42 - 0.5 - 1.5 =
5.8 + 2.35 = 1.5×80 = 0.77÷11 = 12.56÷3.14÷2 =
8.47 - 2.39 = 5 - 0.08 = 3.25 - 1.2 = 0.5÷0.05×0.2 =
0.2×4.9 = 5.3÷0.1 = 1.58 + 5.2 = 3.14×6²÷4 =
9.5÷5 = 1.85×20 = 0.88 + 2.2 = 2÷0.25×3.14 =
0.14×5 = 5.9 - 5.59 = 40×3.14 = 19.8 - 6×0.8 =
6 - 1.35 = 3.7 + 17.3 = 2.7×4 = 13.68 - 3.14 - 3.14 =
答案:
1.3 3 780 62.8
319 1 0.4 1.42
8.15 120 0.07 2
6.08 4.92 2.05 2
0.98 53 6.78 28.26
1.9 37 3.08 25.12
0.7 0.31 125.6 15
4.65 21 10.8 7.4
319 1 0.4 1.42
8.15 120 0.07 2
6.08 4.92 2.05 2
0.98 53 6.78 28.26
1.9 37 3.08 25.12
0.7 0.31 125.6 15
4.65 21 10.8 7.4
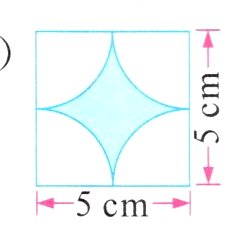
2. 求下面图形涂色部分的面积。
(1)
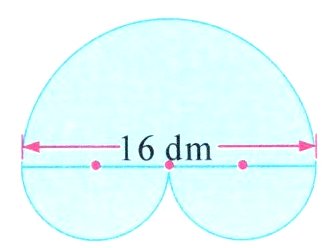
(2)
(3)
(1)

(2)

(3)
答案:
(1)$3.14×3^{2}=28.26(m^{2})$
(2)$5×5 - 3.14×(5÷2)^{2}=5.375(cm^{2})$
(3)$3.14×(16÷2)^{2}÷2 + 3.14×(16÷4)^{2}=150.72(dm^{2})$
(2)$5×5 - 3.14×(5÷2)^{2}=5.375(cm^{2})$
(3)$3.14×(16÷2)^{2}÷2 + 3.14×(16÷4)^{2}=150.72(dm^{2})$
3. 解方程。
5x + 2.2x = 72 0.21x + 8.42 = 9.47 3x + 3.6 - 4.5 = 11.1
5x + 2.2x = 72 0.21x + 8.42 = 9.47 3x + 3.6 - 4.5 = 11.1
答案:
$x = 10$ $x = 5$ $x = 4$
·思维提升 利用面积差不变求线段长度
如图,已知甲比乙的面积大28平方厘米,求AC的长。
二
如图,已知甲比乙的面积大28平方厘米,求AC的长。

二
答案:
$3.14×(40÷2)^{2}÷2 - 28 = 600$(平方厘米)
$600×2÷40 = 30$(厘米)
解析·利用差不变原理可以得到$S_{甲}-S_{乙}=S_{甲}+S_{涂色}-(S_{乙}+S_{涂色})=S_{半圆}-S_{三角形}=28$(平方厘米),所以$S_{三角形}=3.14×(40÷2)^{2}÷2 - 28 = 600$(平方厘米),所以$AC$的长为$600×2÷40 = 30$(厘米)。
$600×2÷40 = 30$(厘米)
解析·利用差不变原理可以得到$S_{甲}-S_{乙}=S_{甲}+S_{涂色}-(S_{乙}+S_{涂色})=S_{半圆}-S_{三角形}=28$(平方厘米),所以$S_{三角形}=3.14×(40÷2)^{2}÷2 - 28 = 600$(平方厘米),所以$AC$的长为$600×2÷40 = 30$(厘米)。
查看更多完整答案,请扫码查看


