22．(本小题满分14分)

　 (理科)已知函数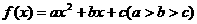的图象上有两点、满足

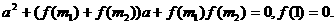
(Ⅰ)求证：；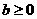

(Ⅱ)求证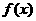：的图象被x轴截得的线段长的取值范围是；

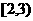(Ⅲ)问能否得出中至少有一个数为正数？证明你的结论.

(文科)已知函数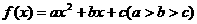的图象上有两点、，满足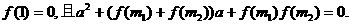

(1)求证：m₁或m₂是方程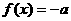的根；

(2)求证：b≥0；

(3)求证：函数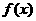的图象被x轴截得的线段长的取值范围是.

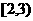21．(本小题满分12分)

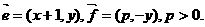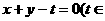(理科)已知曲线C上点M的坐标满足直线l：R)与x轴的交点在曲线C的准线的右边.O为坐标原点.

(1)求证：直线l与曲线C总有两个交点；

(2)设直线l与曲线C的交点为A、B，且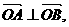求p关于t的函数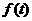的表达式；

(3)在(2)的条件下，若在直线AB上有一点D，使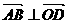，且在t变化时，有

求p的取值范围.

(文科)将抛物线平移后，得曲线C，且直线l：

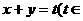R)与x轴的交点在曲线C的准线的右边.

(1)求曲线C的方程；

(2)求证直线与曲线C总有两个交点；

(3)设直线l与曲线C的交点为A、B，且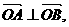求p关于t的函数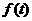的表达式.

20．(本小题满分12分)

甲、乙两人投掷硬币.甲将一枚硬币投掷3次、记正面朝上的次数为ζ；乙将一枚硬币投掷2次，记正面向上的次数为η.

(1)(理)分别求出随机变量ζ和η的数学期望；

　　 (文)求甲在投掷过程中两次正面向上的概率；

(2)若规定ζ>η时甲获胜，求甲获胜的概率.

19．(本小题满分12分)

已知公差大于零的等差数列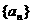的前n项和为S_n，且满足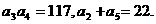

(Ⅰ)求数列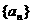的通项公式；

(Ⅱ)若数列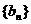是等差数列，且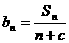，求非零常数c；

(Ⅲ)求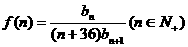的最大值.

18．(本小题满分12分)

在△ABC中，A(cosθ，sinθ)、B(1，0)、C(0，1)(

　 (1)用θ表示△ABC的面积S(θ)；

　 (2)求△ABC面积的最大值；

　 (3)函数y=S(θ)的图象可由函数y=sinθ的图象经过怎样变换得到.

17．(本小题满分12分)

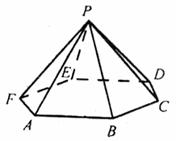　 　　 在正六棱锥P-ABCDEF中，AB=2，PF=.

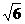求证：(1)PF⊥BD；

　(2)PF⊥平面PBD；

　　　 (3)求二面角F-PA-B的余弦值.

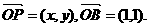16．设O为坐标原点，若点P到x轴、y轴的距离之和既不大于2，又不小于1，则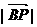的取值范围是　　　　　　　　　 .

15．若函数是定义在R上周期为2的奇函数，则　　　　　 .

14．地球半径为R.若赤道上有A、B两地，经度差为90°，则A、B两地的球面距离为

　　 　　　　　　　　　　.

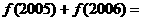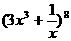13．的展开式的中间一项是为　　　　　　　　　　　　　　 .