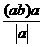18.(本小题共12分)已知点A(0,2)、B(0,4),动点P(x,y)满足
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹与直线y=x+b交与C,D两点,且OC⊥OD(O为原点),求b的值。
19(本小题共12分)参赛号码为1-5号的五名运动员参加射击比赛。
(1) 通过抽签将他们安排到1-5号靶位,试求恰有一名运动员所抽靶位号与其参赛号相同的概率;
(2) 记1号,2号运动员,射击的环数为ξ,(ξ所有取值为0,1,2,…,10),根据教练员提供的资料,其概率分布如下表:
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
P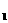 |
0 |
0 |
0 |
0 |
0.05 |
0.05 |
0.05 |
0.2 |
0.3 |
0.32 |
0.03 |
P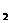 |
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.06 |
0.2 |
0.32 |
0.32 |
0.01 |
①若1,2号运动员个射击一次,求两人中至少一人命中8环的概率;
②试判断,1号,2号运动员谁的射击水平较高?并说明理由。
16.对于函数 给出下列四个命题:
给出下列四个命题:
j该函数的图像关于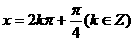 对称
对称
k当且仅当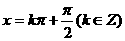 时,该函数取得最大值1;
时,该函数取得最大值1;
l该函数是以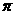 为最小正周期的周期函数;
为最小正周期的周期函数;
m当且仅当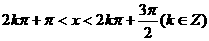 时,
时,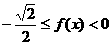 。
。
上述命题中正确的序号是
15.重量为 G牛的重物悬挂在杠杆上距支点A位m米处,杠杆质量分布均匀,单位长度上的重量为q牛,要使加在另一端用来保持在水平平衡且与杠杆垂直的力F最小,杠杆的长度应该是______________
12.已知实系数方程的两根分别为一个椭圆和一个双曲线的离心率,则的取值范围是
A、( -2,-1 ) B、( -1,- 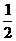 ) C、( -2,-
) C、( -2,- 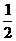 ) D、( -2,+∞ )
) D、( -2,+∞ )
10.函数f(x)=∣log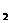 x∣,则f(x)在区间(m,2m+1)(m>0)上不是单调函数的充要条件是
x∣,则f(x)在区间(m,2m+1)(m>0)上不是单调函数的充要条件是
A、0<m<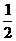 B、0<m<1 C、
B、0<m<1 C、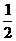 <m<1
D、m>1
<m<1
D、m>1
9. 已知动抛物线以y轴为准线,且恒过点(2,1),则此抛物线顶点的轨迹方程为
A、4(x-1)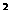 +(y-1)
+(y-1)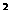 =4 B、(x-2)
=4 B、(x-2)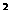 +(y-1)
+(y-1)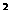 =4 C、(y-1)
=4 C、(y-1)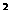 =4(x-1) D、(y-1)
=4(x-1) D、(y-1)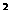 =8(x-2)
=8(x-2)

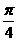 )=,AC=,AB=3.
)=,AC=,AB=3. (n>1,n∈N)的展开式中,含x
(n>1,n∈N)的展开式中,含x ,
,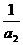 +
+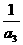 +…..+
+…..+ 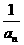 )的值为____________
)的值为____________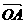 =a ,
=a ,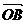 =b,若点B关于所在直线的对称点为B
=b,若点B关于所在直线的对称点为B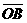 +
+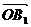 为
为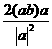 B、
B、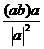 C、
C、 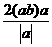 D、
D、