2.箱子里有5个黑球,4个白球,每次从箱中随机取出一个球.若取出的是黑球,则放回箱中,重新取球;若取出的是白球,则停止取球.那么在第4次取球后停止的概率为( )
A. B.
B.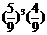 C.
C.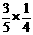 D.
D.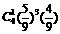
1.(理)复数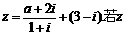 为纯虚数,则实数a= ( )
为纯虚数,则实数a= ( )
A.0 B.-4 C.-6 D.-8
(文)若不等式 ,则实数a= ( )
,则实数a= ( )
A.0 B.-4 C.-6 D.-8
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
在等差数列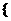
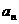
 中,
中, =-14,
=-14, -
- =-14,其中
=-14,其中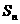 是数列
是数列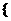
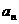
 的前
的前 项之和,曲线
项之和,曲线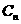 的方程是
的方程是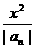 +
+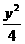 =1,直线
=1,直线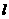 的方程是
的方程是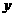 =
=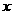 +3.
+3.
(1)求数列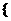
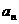
 的通项公式;(2)判断
的通项公式;(2)判断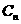 与
与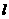 的位置关系;
的位置关系;
(3)当直线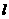 与曲线
与曲线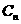 相交于不同的两点
相交于不同的两点 ,
,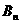 时,令
时,令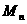 =
=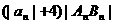 ,求
,求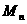 的最小值.
的最小值.
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2006年1月Q型车的销量为 辆,通过分析预测,若以2006年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前
辆,通过分析预测,若以2006年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前 个月的销售总量
个月的销售总量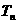 大致满足关系式:
大致满足关系式: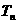 =228
=228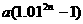 .
.
(1)求Q型车第 个月的月销售量
个月的月销售量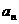 的表达式;
的表达式;
(2)求Q型车前 个月的销售总量
个月的销售总量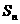 的表达式;
的表达式;
(3)比较两款车前 个月的销售总量
个月的销售总量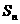 与
与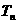 的大小关系.
的大小关系.
解:
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知函数 =
=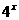 +
+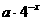 是偶函数.
是偶函数.
(1)求 的值;
的值;
(2)若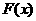 =
=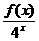 ,用定义证明:
,用定义证明: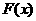 在R上为单调递减函数.
在R上为单调递减函数.
解:
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
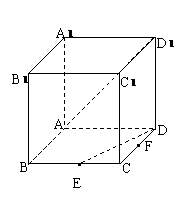 如图,在棱长为1的正方体ABCD-A
如图,在棱长为1的正方体ABCD-A B
B C
C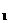 D
D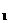 中,E为棱BC的中点.
中,E为棱BC的中点.
(1)求异面直线BD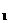 与DE所成角的大小;
与DE所成角的大小;
(2)F是CD的中点,求三棱锥C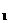 -AEF的体积.
-AEF的体积.
解:
16.关于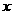 的不等式
的不等式 +4
+4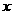 -2
-2 ≤0和
≤0和 -
-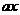 +
+ +3≤0的解集分别是A、B.下列说法中不正确的是( )
+3≤0的解集分别是A、B.下列说法中不正确的是( )
(A)不存在常数 ,使得A、B同时为
,使得A、B同时为 ;
;
(B)至少存在一个常数 ,使得A、B都是仅含有一个元素的集合;
,使得A、B都是仅含有一个元素的集合;
(C)当A、B都是仅含有一个元素的集合时,总有A=B;
(D)当A、B都是仅含有一个元素的集合时,总有A≠B.
15.已知A、B为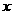 轴上不同的两点,点P的横坐标为1,且|PA|=|PB|,若直线PA的方程为
轴上不同的两点,点P的横坐标为1,且|PA|=|PB|,若直线PA的方程为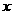 -
-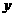 +1=0,则直线PB的方程为(
)
+1=0,则直线PB的方程为(
)
(A)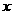 +
+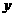 -3=0;(B)
-3=0;(B)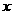 +3
+3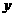 -7=0;(C)
-7=0;(C)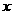 +
+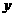 -5=0;(D)2
-5=0;(D)2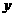 -
-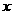 -3=0.
-3=0.

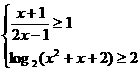 .
.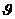 是第四象限的角,且
是第四象限的角,且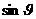 =-
=-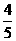 ,求
,求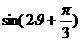 的值.
的值.