科目:,来源:,题型:
18. (本小题满分14分)
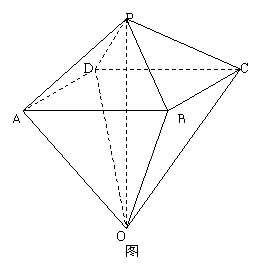
如图4,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
 (Ⅲ)求点P到平面QAD的距离.
(Ⅲ)求点P到平面QAD的距离.
点击展开完整题目
试题详情
科目:,来源:,题型:
17.(本小题满分12分)
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的概率是0.8,计算(结果精确到0.01):
(Ⅰ)恰好有两家煤矿必须整改的概率;
 (Ⅱ)平均有多少家煤矿必须整改;
(Ⅱ)平均有多少家煤矿必须整改;
(Ⅲ)至少关闭一家煤矿的概率.
点击展开完整题目
试题详情
科目:,来源:,题型:
16. (本小题满分12分)
(本小题满分12分)
如图3,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=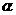 ,∠ABC=
,∠ABC=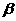 .
.
(Ⅰ)证明  ;
;
(Ⅱ)若AC=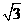 DC,求
DC,求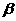 的值.
的值.
点击展开完整题目
试题详情
科目:,来源:,题型:
9. 棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图1,则图中三角形(正四面体的截面)的面积是 (
)
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图1,则图中三角形(正四面体的截面)的面积是 (
)
A. B.
B.
C.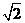 D.
D.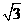
点击展开完整题目
试题详情

 如图2,OM∥AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界)运动,且
如图2,OM∥AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界)运动,且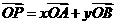 ,则
,则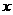 的取值范围是
;
的取值范围是
; 时,
时, 的取值范围是
.
的取值范围是
. 
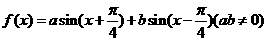 是偶函数,则有序实数对(
是偶函数,则有序实数对( )可以是
.(注:只要填满足
)可以是
.(注:只要填满足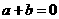 的一组数即可)(写出你认为正确的一组数即可).
的一组数即可)(写出你认为正确的一组数即可). 和
和 在它们交点处的两条切线与
在它们交点处的两条切线与 则
则 的最小值是
.
的最小值是
. 的展开式中
的展开式中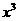 的系数是-80,则实数
的系数是-80,则实数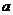 的值是
.
的值是
. 上至少有三个不同点到直线
上至少有三个不同点到直线 :
: 的距离为
的距离为 ,则直线
,则直线 ] B.[
] B.[ ]
C.[
]
C.[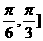 D.
D.
