9.若动点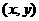 在曲线
在曲线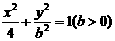 上变化,则
上变化,则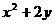 的最大值为 ( )
的最大值为 ( )
A.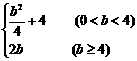 B.
B.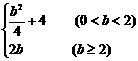
C.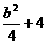 D.
D.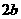
解:由题意可设x=2cosα,y=bsinα,则x2+2y=4cos2α+2bsinα=-4sin2α+2bsinα+4
=-2(sin2α-bsinα-2)=-2(sinα-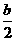 )2+4+
)2+4+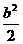 ,∴
,∴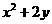 的最大值为
的最大值为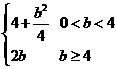 ,选(A)
,选(A)
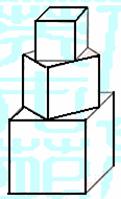 10.有一塔形几何体由若干个正方体构成,构成方式如图所
10.有一塔形几何体由若干个正方体构成,构成方式如图所
示,上层正方体下底面的四个顶点是下层正方体上底面
各连接中点,已知最底层正方体的棱长为2,且该塔形
的表面积(含最底层正方体的底面面积)超过39,则
该塔形中正方体的个数至少是 ( )
A.4 B.5
C.6 D.7
解:k层塔形的各层立方体的边长,增加的表面积以及k层塔形的
表面积一览表如下:
|
第k个立方体边长ak |
a!=2 |
a2=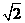 |
a3=1 |
a4=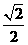 |
a5= 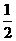 |
a6= 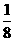 |
|
第k层立方体增加的面积bk |
b1=24 |
b2=8 |
b3=4 |
b4=2 |
b5=1 |
b6=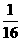 |
|
K层塔形的表面积Sk |
S1=24 |
S2=32 |
S3=36 |
S4=38 |
S5=39 |
S6=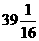 |
由上表可以看出要使塔形的表面积(含最底层正方体的底面面积)超过39,则
该塔形中正方体的个数至少是6层,选(C)
8.若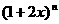 展开式中含
展开式中含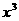 的项的系数等于含x的项的系数的8倍,则n等于 ( )
的项的系数等于含x的项的系数的8倍,则n等于 ( )
A.5 B.7 C.9 D.11
解: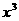 的项的系数为
的项的系数为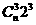 ,x的项的系数为
,x的项的系数为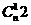 ,由题意得
,由题意得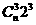 =8
=8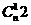 解之得n=5,选(A)一了
解之得n=5,选(A)一了
7.对于不重合的两个平面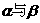 ,给定下列条件:
,给定下列条件:
①存在平面 ,使得α、β都垂直于
,使得α、β都垂直于 ;
;
②存在平面 ,使得α、β都平行于
,使得α、β都平行于 ;
;
③存在直线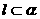 ,直线
,直线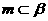 ,使得
,使得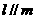 ;
;
④存在异面直线l、m,使得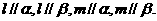
其中,可以判定α与β平行的条件有 ( )
A.1个 B.2个 C.3个 D.4个
解:命题①③是真命题,选(B)
6.已知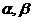 均为锐角,若
均为锐角,若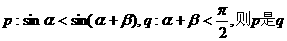 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解:∵由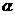 、
、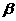 均为锐角,
均为锐角,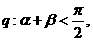 得0<α<α+β<
得0<α<α+β<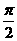 ∴sin(α+β)>sinα,但
∴sin(α+β)>sinα,但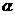 、
、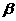 均为锐角,sinα<sin(α+β),不一定能推出α+β<
均为锐角,sinα<sin(α+β),不一定能推出α+β<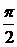 ,如α=
,如α=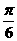 ,β=
,β=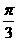 就是一个反例,选(C)
就是一个反例,选(C)
5.不等式组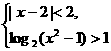 的解集为 ( )
的解集为 ( )
A.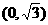 B.
B.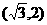 C.
C.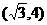 D.
D.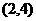
解∵|x-2|<2的解集为(0,4),log2(x2-1)>1的解集为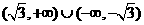 ,∴不等式组
,∴不等式组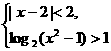 的解集
的解集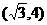 ,选(C)
,选(C)
4.设向量a=(-1,2),b=(2,-1),则(a·b)(a+b)等于 ( )
A.(1,1) B.(-4,-4) C.-4 D.(-2,-2)
解:(a·b)(a+b)=[-2+(-2)](1,1)=(-4,-4),选(B)
3.若函数 是定义在R上的偶函数,在
是定义在R上的偶函数,在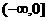 上是减函数,且
上是减函数,且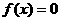 ,则使得
,则使得
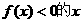 的取值范围是 ( )
的取值范围是 ( )
A.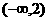 B.
B.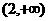
C. D.(-2,2)
D.(-2,2)
解:∵函数 是定义在R上的偶函数,在
是定义在R上的偶函数,在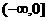 上是减函数,且
上是减函数,且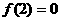 ,∴f(-2)=0, 在
,∴f(-2)=0, 在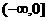 上
上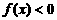 的x的取值范围是
的x的取值范围是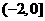 ,又由对称性
,又由对称性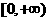 ,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
1.圆 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )
A.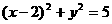 B.
B.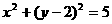
C.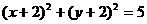 D.
D.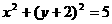
解:∵圆 的圆心(-2,0)关于原点对称的点为(2,0),∴圆
的圆心(-2,0)关于原点对称的点为(2,0),∴圆 关于原点对称的圆为(x-2)2+y2=5,选(A).
关于原点对称的圆为(x-2)2+y2=5,选(A).
22.(本小题12分)
(Ⅰ)证明:(1)当n=2时,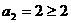 ,不等式成立.
,不等式成立.
(2)假设当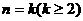 时不等式成立,即
时不等式成立,即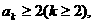
那么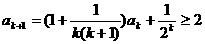 . 这就是说,当
. 这就是说,当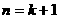 时不等式成立.
时不等式成立.
根据(1)、(2)可知: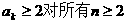 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有
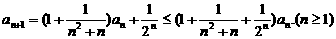
两边取对数并利用已知不等式得
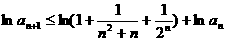
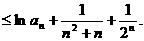 故
故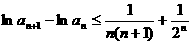
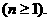
上式从1到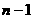 求和可得
求和可得
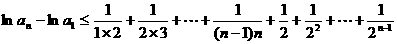
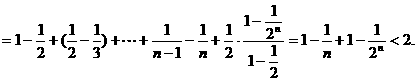
即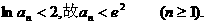
(Ⅱ)证法二:
由数学归纳法易证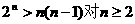 成立,故
成立,故
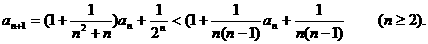
令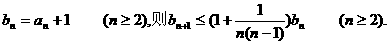
取对数并利用已知不等式得 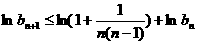
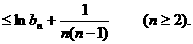
上式从2到n求和得 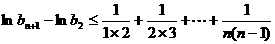
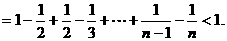
因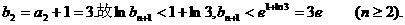
故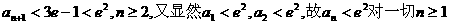 成立.
成立.

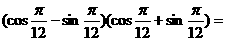 ( )
( )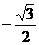 B.
B.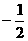 C.
C.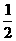 D.
D.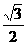
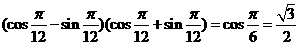 ,选(D)
,选(D)