22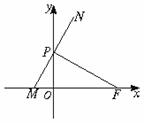．(本题满分14分)如图，点F(a，0)(a>0)，点P在y轴上运动，M在x轴上，N为动点，且0.

(1)求点N的轨迹C的方程；

(2)过点F(a，0)的直线l(不与x轴垂直)与曲线C交于A、B两点，设点K(－a，0)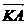，与的夹角为θ，

求证：0<θ<.

21．(本题满分12分)已知函数f(x)=－x³+3x²+ax+b在x＝(1，f(1))处的切线与直线12x－y－1＝0平行．

(1)求实数a的值；

(2)求f(x)的单调递减区间；

(3)若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．

20．(本小题满分12分)

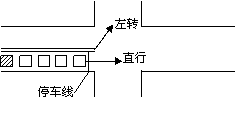如图，一辆车要通过某十字路口，直行时前方

刚好由绿灯转为红灯，该车前面已有4辆车依次在

同一车道上排队等候(该车道只可以直行或左转行

驶)。已知每辆车直行的概率是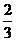，左转行驶的概率

是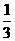，该路口红绿灯转换间隔均为1分钟。假设该车道上一辆直行的车驶出停车线需要10秒，一辆左转的车驶出停车线需要20秒，求：

(1)前4辆恰有2辆左转行驶的概率；

(2)该车在第一次绿灯亮起时的1分钟内通过该路口的概率；(汽车驶出停车线就算通过路口)

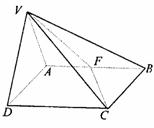
19．(本题满分12分)如图，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB∶AD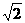＝∶1，F是AB的中点．

(1)求VC与平面ABCD所成的角；

(2)求二面角V-FC-B的度数；

(3)当V到平面ABCD的距离是3时，求B到平面VFC的距离．

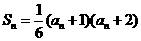18．(本题满分12分) 已知数列{a_n}的各项均为正数，且前n项和S_n满足．若a₂、a₄、a₉ 成等比数列，求数列{a_n}的通项公式．

17．(本题满分12分)已知f(x)=4msinx - cos2x　 (x∈R)，若f(x)的最大值为3，求实数m的值。

13、　　　　　 　14、　　　　 　15、　　　　 16、　　　　 　

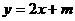16．直线和圆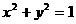交于A和B，以OX为始边，OA、OB为终边的角分别为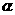、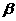，则sin(+)的值为　　　　 .

第二卷

填空题答题栏

15．如图，A，B，C，D为海上的四个小岛，要建三座桥，将这四个小岛连接起来，则不同的建桥方案共有__________.(用数字作答)

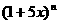14.若与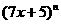的展开式中各项系数之和分别为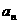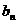，，则=　　　 .
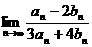