12.设函数f(x)的定义域为R,若存在常数M>0,使|f(x)|≤M|x|对于一切实数x均成立,则称f(x)为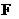 函数,给出下列函数:① f(x)=0;② f(x)=x2;③ f(x)=
函数,给出下列函数:① f(x)=0;② f(x)=x2;③ f(x)= (sinx+cosx);④
(sinx+cosx);④ 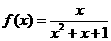 ;⑤ f(x)是定义在R上的奇函数,且满足对于一切实数x1, x2,均有|f(x1)-f(x2)|≤2|x1-x2|,其中是
;⑤ f(x)是定义在R上的奇函数,且满足对于一切实数x1, x2,均有|f(x1)-f(x2)|≤2|x1-x2|,其中是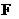 函数的序号是
。
函数的序号是
。
11.设双曲线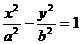 (a>0, b>0)的焦距为2c,A、B分别为实轴与虚轴的一个端点,若坐标原点到直线AB的距离为
(a>0, b>0)的焦距为2c,A、B分别为实轴与虚轴的一个端点,若坐标原点到直线AB的距离为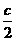 ,则双曲线的离心率为
;渐近线方程为
。
,则双曲线的离心率为
;渐近线方程为
。
21.(本小题满分16分)
已知椭圆C1: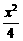 +y2=1的左、右顶点分别是A、B,点P是双曲线C2:
+y2=1的左、右顶点分别是A、B,点P是双曲线C2: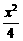 -y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
-y2=1在第一象限部分上的一点,连结AP交椭圆C1于点C,连结PB并延长交椭圆C1于点D.
(1)若直线PA与PB的斜率分别为k1、k2,求证:k1·k2是定值;
(2)若△ACD与△PCD的面积相等,求直线CD的倾斜角;
(3)直线CD的倾斜角是否会随着点P的不同而改变?并说明理由.
20.(本小题满分16分)
已知集合A={(x,y)|y≥|x-a|},B={(x,y)|y≤-a|x|+2a}(a≥0).
(1)证明A∩B≠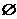 ;
;
(2)当0≤a≤4时,求由A∩B中点组成图形面积的最大值.
19.(本小题满分12分)
如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第i行第j列的数为aij(i≥j,i、j∈N*).
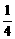
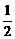 ,
,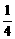
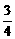 ,
,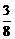 ,
,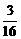
……
(1)试写出aij关于i、j的表达式,并求a83;
(2)设这个数阵共有n行,求数阵表中的所有数之和.
18.(本小题满分14分)
在正四棱柱ABCD-A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的一点.
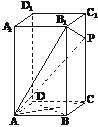
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的正切值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线?

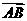 =(1, 0),
=(1, 0),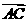 =(2, 2),则
=(2, 2),则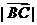 =
。
=
。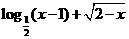 的定义域为
。
的定义域为
。