7.2003年9月1日,某中学按年利率5%(利息按年以复利计算)从银行贷款500万元,用于建造一所可容纳1000人住宿的学生公寓,2004年9月1日投入使用,同时向每位学生收取一年住宿费a元用于还贷,照此方式,预计15年还清贷款,则a的值约为(提供:1.0515≈2.08)
A.412 B.482 C.500 D.512
6. 已知函数f(x)=sinπx的图象的一部分如图(a),有以下四个函数解析式:
①y=f(2-x);②y=f(x+1);③y=f(x-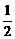 );④y=f(-x+1).
);④y=f(-x+1).
其中与图(b)所对应的函数解析式为
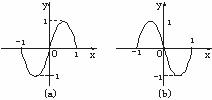
A.①② B.②③ C.③④ D.①④
4.函数f(x)=b(1-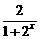 )+sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
)+sinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在
(-∞,0)上有
A.最大值10 B.最小值-5 C.最小值-4 D.最大值13
3. .已知|p|=2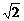 ,|q|=3,p、q的夹角为
,|q|=3,p、q的夹角为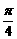 ,如下图所示,若
,如下图所示,若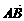 =5p+2q,
=5p+2q,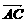 =p-3q,且D为BC的中点,则
=p-3q,且D为BC的中点,则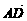 的长度为
的长度为

A.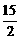 B.
B.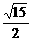 C.7 D.8
C.7 D.8
2. 下表是某市7个县级行政管理区人口数与土地面积:
|
行政区代号 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
人口(万) |
63.46 |
59.44 |
103.23 |
38.11 |
21.67 |
6.46 |
6.61 |
|
面积(万 km2) |
0.33 |
0.20 |
0.45 |
0.15 |
0.07 |
0.02 |
0.02 |
经统计比较可知,其中人口密度(人口/面积)最大的行政区是
A.x2 B.x3 C.x5 D.x7
1.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是
A.81.2,4.4 B.78.8,4.4 C.81.2,84.4 D.78.8,75.6
22.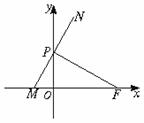 (本题满分14分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,且
(本题满分14分)如图,点F(a,0)(a>0),点P在y轴上运动,M在x轴上,N为动点,且 0.
0.
(1)求点N的轨迹C的方程;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点K(-a,0),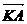 与
与 的夹角为θ,
的夹角为θ,
求证:0<θ<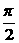 .
.
21.(本题满分12分)已知函数f(x)=-x3+3x2+ax+b在x=(1,f(1))处的切线与直线12x-y-1=0平行.
(1)求实数a的值;
(2)求f(x)的单调递减区间;
(3)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
20.(本小题满分12分)
 如图,一辆车要通过某十字路口,直行时前方
如图,一辆车要通过某十字路口,直行时前方
刚好由绿灯转为红灯,该车前面已有4辆车依次在
同一车道上排队等候(该车道只可以直行或左转行
驶)。已知每辆车直行的概率是 ,左转行驶的概率
,左转行驶的概率
是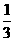 ,该路口红绿灯转换间隔均为1分钟。假设该车道上一辆直行的车驶出停车线需要10秒,一辆左转的车驶出停车线需要20秒,求:
,该路口红绿灯转换间隔均为1分钟。假设该车道上一辆直行的车驶出停车线需要10秒,一辆左转的车驶出停车线需要20秒,求:
(1)前4辆恰有2辆左转行驶的概率;
(2)该车在第一次绿灯亮起时的1分钟内通过该路口的概率;(汽车驶出停车线就算通过路口)

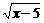 ≠kx对一切x≥15均成立,则有
≠kx对一切x≥15均成立,则有 C.k≤0或k>
C.k≤0或k>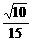 D.0≤k<
D.0≤k<