《2025年成才之路高中新课程学习指导高中数学选择性必修第二册人教版》

11. 已知数列$\{ a_{n}\}$满足$a_{1}=15$，且$3a_{n+1}=3a_{n}-2$，则$a_{k}· a_{k+1}＜0$的$k$值为23.

答案： 11. 23 因为$3a_{n + 1}=3a_{n}-2$，所以$a_{n + 1}-a_{n}=-\frac{2}{3}$，所以数列$\{a_{n}\}$是首项为$15$，公差为$-\frac{2}{3}$的等差数列，所以$a_{n}=15-\frac{2}{3}·(n - 1)=-\frac{2}{3}n+\frac{47}{3}$。令$a_{n}=-\frac{2}{3}n+\frac{47}{3}\gt0$，得$n\lt23.5$，又$k\in\mathbf{N}^{*}$，所以使$a_{k}· a_{k + 1}\lt0$的$k$值为$23$。

12. 已知正项数列$\{ a_{n}\}$满足$a_{1}=1$，$a_{n}^{2}+a_{n+2}^{2}=2a_{n+1}^{2}$，且$a_{4}-a_{2}=\frac {2}{a_{4}+a_{2}}$.
(1)求数列$\{ a_{n}^{2}\}$的通项公式；
(2)求满足不等式$a_{n+5}+1＜2a_{n}$的正整数$n$的最小值.

答案： 12.【解析】
(1)由已知得$a_{n + 2}^{2}-a_{n + 1}^{2}=a_{n + 1}^{2}-a_{n}^{2}$，
所以数列$\{a_{n}^{2}\}$是等差数列，设其公差为$d$。
由$a_{4}-a_{2}=\frac{2}{a_{4}+a_{2}}$，得$a_{4}^{2}-a_{2}^{2}=2$。
所以$2d = 2$，即$d = 1$，
所以$a_{n}^{2}=a_{1}^{2}+(n - 1)d=n$。
(2)由$a_{n}\gt0$，得$a_{n}=\sqrt{n}$，
所以原不等式可化为$\sqrt{n + 5}+1\lt2\sqrt{n}$，
两边平方可得$n + 6 + 2\sqrt{n + 5}\lt4n$，
即$2\sqrt{n + 5}\lt3n - 6$，
所以$4(n + 5)\lt(3n - 6)^{2}$，
整理得$(n - 4)(9n - 4)\gt0$，
解得$n\gt4$或$n\lt\frac{4}{9}$。
因为$n\in\mathbf{N}^{*}$，故$n$的最小值为$5$。

13. 甲虫是行动较快的昆虫之一，下表记录了某种类型的甲虫的爬行距离：

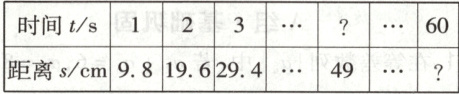
(1)你能建立一个等差数列的模型，表示甲虫的爬行距离和时间之间的关系吗？
(2)利用建立的模型计算，甲虫1min能爬多远？它爬行49cm需要多长时间？

答案： 13.【解析】
(1)由题表中数据可知，该数列从第$2$项起，每一项与前一项的差都是常数$9.8$，
所以该模型是一个等差数列模型。因为$a_{1}=9.8$，$d = 9.8$，
所以甲虫的爬行距离$s$与时间$t$的关系是$s = 9.8t$。
(2)当$t = 1\min = 60\mathrm{s}$时，
$s = 9.8t = 9.8×60 = 588(\mathrm{cm})$。
当$s = 49\mathrm{cm}$时，$t=\frac{s}{9.8}=\frac{49}{9.8}=5(\mathrm{s})$。

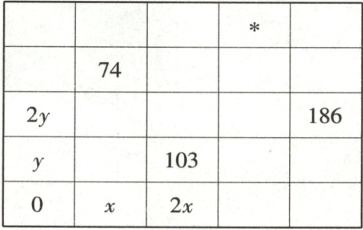
14. 在下表所示的$5× 5$正方形的25个空格中填入正整数，使得每一行、每一列都成等差数列，则标有*号的空格应填的数是142.

答案： 14. 142 记$a_{ij}$为第$i$行第$j$列的格中所填的数，则$a_{32}=x$，$a_{44}=y$。
由第$3$行得$a_{33}=\frac{2y + 186}{2}$，由第$3$列得$a_{33}=2×103 - 2x$，所以$2x + y = 113$。①，由第$1$列得$a_{21}=3y$，则由第$2$行得$a_{23}=2×74 - 3y$，由第$3$列得$a_{33}+103=a_{23}+2x$，则$a_{23}=3×103 - 4x$，所以$2×74 - 3y = 3×103 - 4x$，即$4x - 3y = 161$②，联立①②，得$x = 50$，$y = 13$，所以$a_{15}=2×186 - a_{35}=2×186 - 4x = 172$，$a_{13}=2a_{33}-a_{53}=112$，$a_{14}=\frac{a_{13}+a_{15}}{2}=142$，故标有$*$号的空格应填$142$。