5. 正多边形的中心角都
相等
,如果一个正多边形的中心角是$45^{\circ}$,那么这个正多边形是正八
边形.
答案:
5.相等 八
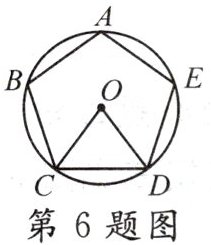
6. (2024·仙桃模拟)如图,正五边形$ABCDE$内接于$\odot O$,连接$OC$,$OD$,则$\angle BAE-\angle COD=$(
A.$60^{\circ}$
B.$54^{\circ}$
C.$48^{\circ}$
D.$36^{\circ}$
D
)
A.$60^{\circ}$
B.$54^{\circ}$
C.$48^{\circ}$
D.$36^{\circ}$
答案:
6.D
7. [新课标·数学文化](2024·重庆期末)刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了我国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若$\odot O$的半径为$1$,则这个圆内接正十二边形的面积为(

A.$3$
B.$\pi$
C.$4$
D.$2\pi$
A
)
A.$3$
B.$\pi$
C.$4$
D.$2\pi$
答案:
7.A
8. 如图,正六边形$ABCDEF$内接于$\odot O$,已知$\odot O$的半径为$4$,则这个正六边形的边长$BC=$
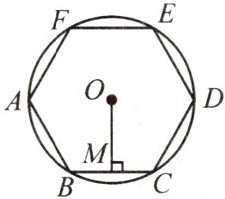
4
,边心距$OM=$$2\sqrt{3}$
.
答案:
8.4 $2\sqrt{3}$
9. 如图,正方形$ABCD$内接于$\odot O$,$P$为$\overset{\frown}{BC}$上的一点,连接$DP$,$CP$.求$\angle CPD$的度数.


答案:
9.解:连接OD,OC.
∵正方形ABCD内接于⊙O,
∴∠DOC = $90^{\circ}$.
∴∠DPC = $\frac{1}{2}$∠DOC = $45^{\circ}$.

9.解:连接OD,OC.
∵正方形ABCD内接于⊙O,
∴∠DOC = $90^{\circ}$.
∴∠DPC = $\frac{1}{2}$∠DOC = $45^{\circ}$.

10. 如图,正八边形$ABCDEFGH$内接于$\odot O$,$P$为弧$AB$上的一点(点$P$不与点$A$,$B$重合),求$\angle DPF$的度数.


答案:
10.解:如图,连接OD、OE、OF,
∵八边形ABCDEFGH是正八边形,
∴∠DOE = ∠EOF = $\frac{360^{\circ}}{8}$ = $45^{\circ}$.
∴

∠DOF = ∠DOE + ∠EOF = $90^{\circ}$.
∴∠DPF = $\frac{1}{2}$∠DOF = $45^{\circ}$.
10.解:如图,连接OD、OE、OF,
∵八边形ABCDEFGH是正八边形,
∴∠DOE = ∠EOF = $\frac{360^{\circ}}{8}$ = $45^{\circ}$.
∴

∠DOF = ∠DOE + ∠EOF = $90^{\circ}$.
∴∠DPF = $\frac{1}{2}$∠DOF = $45^{\circ}$.
11. [教材 P106 知识综合]下列说法:①正$n$边形的中心角为$\frac{360^{\circ}}{n}$;②正$n$边形的每个内角为$\frac{(n - 2)·180^{\circ}}{n}$;③正$n$边形的每个外角为$\frac{360^{\circ}}{n}$;④正$n$边形的半径$R$、边心距$r$和边长$a_n$满足关系式:$R^2 = r^2+\frac{1}{4}a_n^2$.其中正确的有(
A.$1$个
B.$2$个
C.$3$个
D.$4$个
D
)A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
11.D
12. 若正方形的外接圆半径为$2$,则其内切圆半径为(
A.$\sqrt{2}$
B.$2\sqrt{2}$
C.$\frac{\sqrt{2}}{2}$
D.$1$
A
)A.$\sqrt{2}$
B.$2\sqrt{2}$
C.$\frac{\sqrt{2}}{2}$
D.$1$
答案:
12.A
13. 半径为$R$的圆的内接正三角形、正六边形的边心距之比为(
A.$1:\sqrt{2}$
B.$1:2$
C.$1:\sqrt{3}$
D.$\sqrt{3}:1$
C
)A.$1:\sqrt{2}$
B.$1:2$
C.$1:\sqrt{3}$
D.$\sqrt{3}:1$
答案:
13.C
查看更多完整答案,请扫码查看


