《2025年胜券在握同步解析与测评三年级数学上册人教版重庆专版》

5. 观察下面的图形，数一数，画一画，填一填。

根据你发现的规律，再往后的一个图形一共有多少个角？

答案： 1. 首先计算前三个图形角的数量：
对于$2 + 1$：
$2+1 = 3$（个）。
对于$3 + 2+1$：
$3 + 2+1=(3 + 1)+2=4 + 2=6$（个）。
2. 然后找规律：
设射线的数量为$n$（$n\geqslant2$），角的数量公式为$\frac{n(n - 1)}{2}$（从$n$条射线中选$2$条射线组成角，组合数公式$C_{n}^2=\frac{n!}{2!(n - 2)!}=\frac{n(n - 1)}{2}$）。
第一个图$n = 2$，$\frac{2×(2 - 1)}{2}=1$；第二个图$n = 3$，$\frac{3×(3 - 1)}{2}=\frac{3×2}{2}=3$；第三个图$n = 4$，$\frac{4×(4 - 1)}{2}=\frac{4×3}{2}=6$。
第四个图$n = 5$。
3. 最后计算第四个图角的数量：
根据公式$\frac{n(n - 1)}{2}$，当$n = 5$时，$\frac{5×(5 - 1)}{2}=\frac{5×4}{2}=10$，也可以用$4+3+2+1=(4 + 1)+(3 + 2)=5 + 5 = 10$（个）。
故答案依次为：$1$；$3$；$6$；$4 + 3+2+1 = 10$，$10$。

6. 用放大镜观察下面的角，角的大小会发生什么变化？

答案： 6.角的大小不变。

7. 小红、小丽和小亮比赛剪纸，在正方形纸上剪掉一个角，看谁剩下的角多。根据他们的排名画一画，填一填。(将剩余部分涂色)

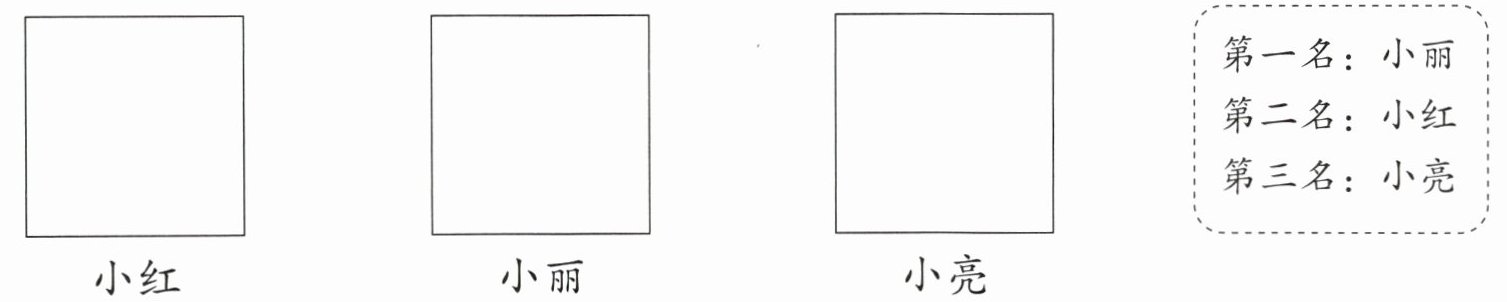
小红 小丽 小亮
剩下(5)个角 剩下(4)个角 剩下(3)个角
]

答案：
7.(答案不唯一)　　　　　　 4 5 3