第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4. 方方从家出发去学校有三条路可以走(如图),哪条路最近?说说你的理由。
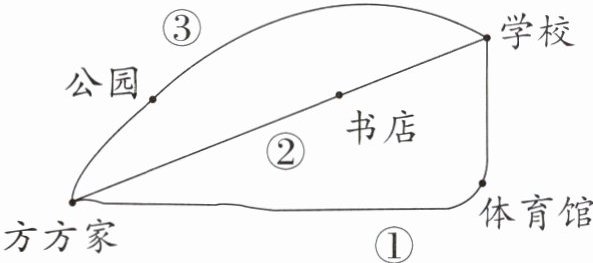

答案:
4.第②条路最近。因为两点间所有连线中线段最短。
5. 画一画,填一填。
(1) 经过一点,能画( )条直线。
(2) 经过两点,能画( )条直线。
(3) 在下面各图中每两个点之间画一条直线(经过这两点),分别最多能画几条?
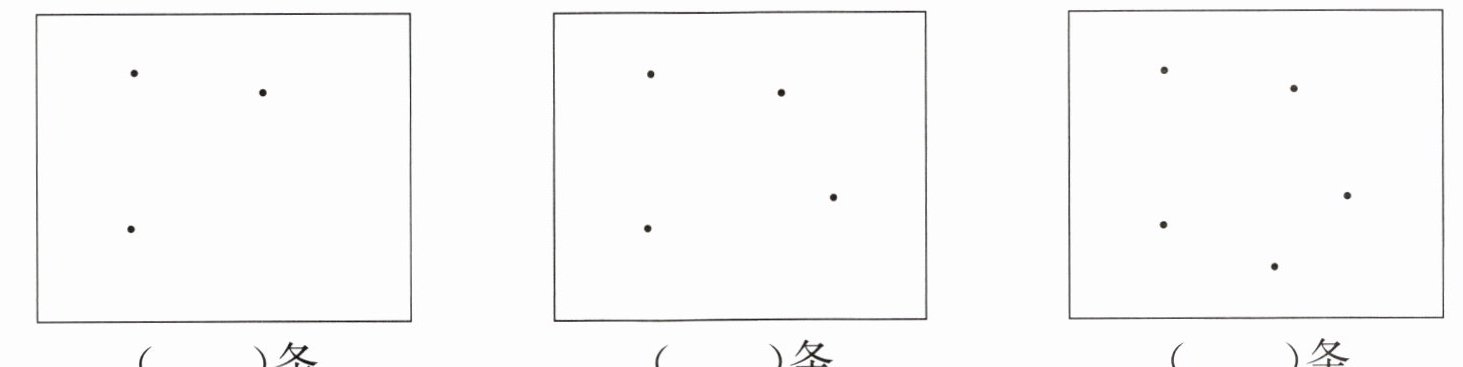
(1) 经过一点,能画( )条直线。
(2) 经过两点,能画( )条直线。
(3) 在下面各图中每两个点之间画一条直线(经过这两点),分别最多能画几条?

答案:
5.
(1)无数
(2)1
(3)

3 6 10
5.
(1)无数
(2)1
(3)

3 6 10
6. 下面的图形中分别有几条线段?数一数,填一填。

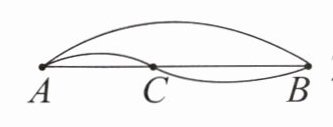
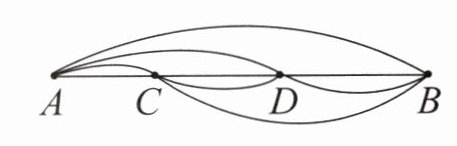

我发现:。
当直线 $l$ 上有 10 个点时,在这条直线上可以数出( )条线段。




我发现:。
当直线 $l$ 上有 10 个点时,在这条直线上可以数出( )条线段。
答案:
1. 对于第一个图:
两点$A$、$B$,根据线段的定义,两点确定一条线段,所以有$1$条线段。
2. 对于第二个图:
公式$2 + 1$,$2+1 = 3$(条)。
3. 对于第三个图:
公式$3 + 2+1$,$3 + 2+1=6$(条)。
4. 对于第四个图:
有$4$个间隔,公式为$4 + 3+2 + 1$,$4 + 3+2 + 1 = 10$(条)。
发现:当直线上有$n$个点时,线段的总条数是$1 + 2+3+\cdots+(n - 1)=\frac{n(n - 1)}{2}$($n\geqslant2$)。
5. 当$n = 10$时:
根据公式$\frac{n(n - 1)}{2}$,把$n = 10$代入$\frac{n(n - 1)}{2}=\frac{10×(10 - 1)}{2}$。
先算$10×(10 - 1)=10×9 = 90$,再算$90÷2 = 45$。
故答案依次为:$1$;$3$;$6$;$4 + 3+2 + 1$,$10$;$45$。
两点$A$、$B$,根据线段的定义,两点确定一条线段,所以有$1$条线段。
2. 对于第二个图:
公式$2 + 1$,$2+1 = 3$(条)。
3. 对于第三个图:
公式$3 + 2+1$,$3 + 2+1=6$(条)。
4. 对于第四个图:
有$4$个间隔,公式为$4 + 3+2 + 1$,$4 + 3+2 + 1 = 10$(条)。
发现:当直线上有$n$个点时,线段的总条数是$1 + 2+3+\cdots+(n - 1)=\frac{n(n - 1)}{2}$($n\geqslant2$)。
5. 当$n = 10$时:
根据公式$\frac{n(n - 1)}{2}$,把$n = 10$代入$\frac{n(n - 1)}{2}=\frac{10×(10 - 1)}{2}$。
先算$10×(10 - 1)=10×9 = 90$,再算$90÷2 = 45$。
故答案依次为:$1$;$3$;$6$;$4 + 3+2 + 1$,$10$;$45$。
查看更多完整答案,请扫码查看


