《2025年同步练习江苏九年级物理上册苏科版》

1. 在使用简单机械时,为了达到目的必须要做的功称为有用功；并非我们所需要的,但又不得不做的功称为额外功；利用机械做的全部的功称为总功。

答案： 有用 额外 总

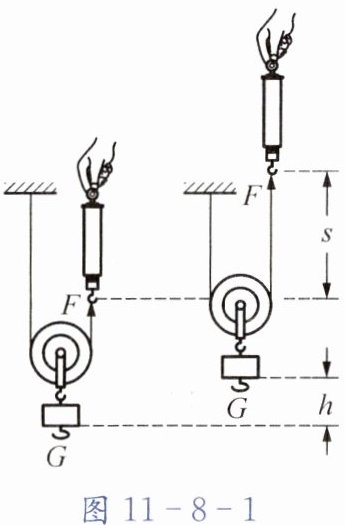
2. 如图11-8-1所示,在使用动滑轮提起重物时,若钩码的重力是$G$,弹簧测力计的拉力是$F$,重物上升的高度是$h$,弹簧测力计拉绳子移动的距离是$s$,则有用功$W_{有用}= $Gh,$W_{总}= $Fs。若用$W_{有用}和W_{总}$来表示额外功,则$W_{额外}= $$W_{总}-W_{有用}$。

答案： Gh Fs W总 - W有

3. 物理学中,将有用功与总功的比叫作机械效率,可以用公式表示为$\eta=$$\frac {W_{有用}}{W_{总}}×100\%$。

答案： 有用 总 $\frac {W_{有用}}{W_{总}}×100\%$

4. 如图11-8-2所示是测量动滑轮机械效率的部分实验装置。
(1)需要测量的物理量有：①被提升的钩码重G、②钩码被提升的高度h、③拉力F、④拉力移动的距离s。
(2)需要的实验器材有：① 铁架台、② 动滑轮和细绳、③ 钩码、④弹簧测力计、⑤刻度尺。

答案：
(1)① 被提升的钩码重G ② 钩码被提升的高度h ③ 拉力F ④ 拉力移动的距离s
(2)④ 弹簧测力计 ⑤ 刻度尺

5. 在使用简单机械做功的过程中,因为额外功$W_{额外}$＞0,所以$W_{总}$＞$W_{有用}$,故机械效率$\eta$＜100%。

答案： ＞ ＞ ＜

6. 若某人使用一个简单机械所做的总功是10000 J,其中额外功是2500 J,则有用功是7500J,机械效率是75%。

答案： 7500 75%

7. 如图11-8-3所示,甲、乙、丙三人用三种方法把沙子运上三楼,根据图中的数据可算出三种方法所做的有用功的大小均为600J,所做总功最多的是甲(甲/乙/丙),他所做的功为3120J。

答案： 600 甲 3120

8. 下列说法中正确的是(D)。
A.做的有用功越多,机械效率越高
B.做的额外功越多,机械效率越低
C.做的总功越少,机械效率越高
D.额外功占总功的比例越大,机械效率越低

答案： D

9. 甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,(B)。
A.甲吊车做的有用功较多
B.乙吊车做的额外功较多
C.甲吊车做的总功较多
D.甲、乙两吊车做的总功相同

答案： B