实验目的
经历用小棒摆三角形和正方形的过程,体会不同摆法与所用小棒根数之间的关系,感受拼摆的乐趣。
实验准备
第46页中的小棒。
实验过程
1 摆摆数数
摆1个三角形要用3根小棒,摆2个三角形要用多少根小棒?
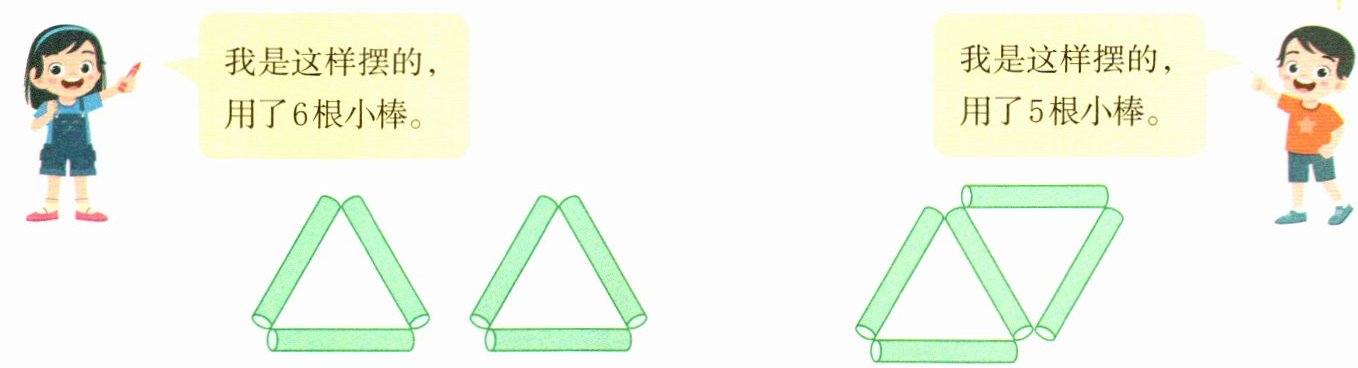
为什么用5根小棒也能摆出2个三角形?
2 想想摆摆
(1)用小棒摆3个三角形,可以怎样摆?最少要用多少根小棒?
(2)用11根小棒摆三角形,可以怎样摆?最多能摆出多少个同样的三角形?
3 摆摆比比
(1)摆4个同样的正方形,要用多少根小棒?
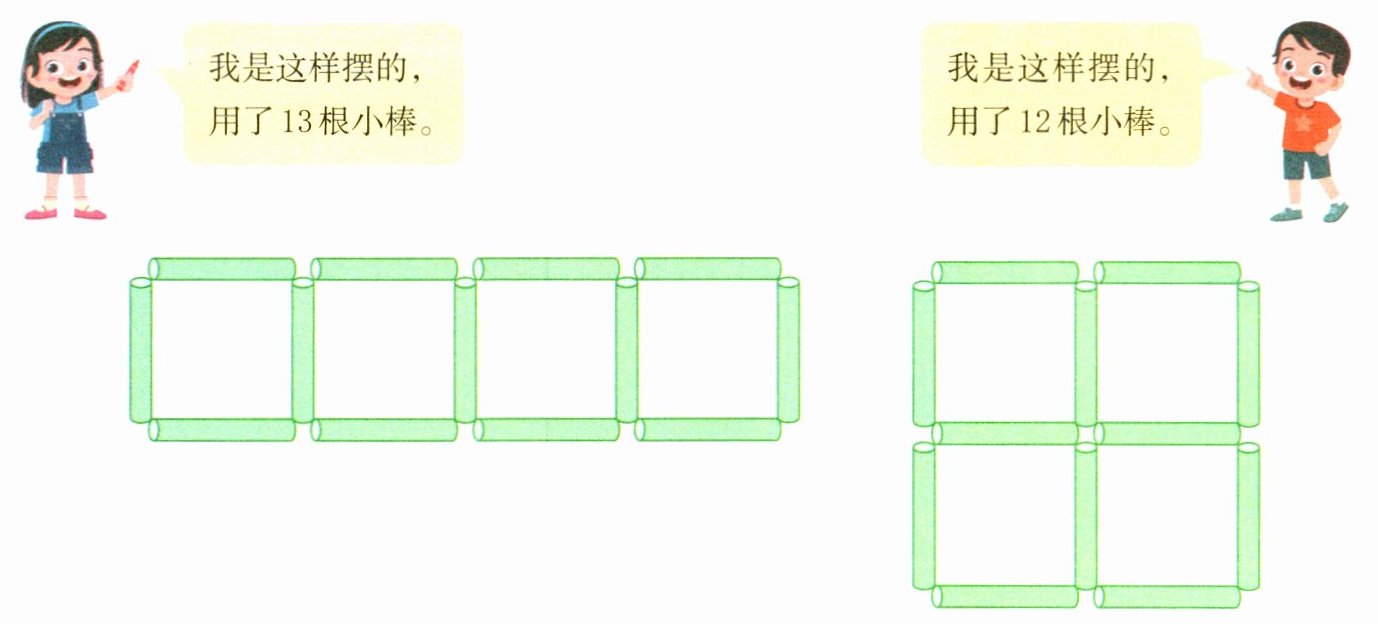

4 回顾反思
用小棒摆三角形或正方形,要想所用小棒的根数尽量少,你有什么好办法?
本实验可以在学习二年级上册“1~6的表内乘法”时进行。
“摆摆数数”是用小棒摆出2个三角形,感受不同摆法所用小棒的根数不一样。
“想想摆摆”继续用小棒摆三角形,先是摆出指定个数的三角形,接着用指定根数的小棒摆出尽量多的三角形,鼓励学生探索不同的摆法。
“摆摆比比”是用小棒摆正方形,在不同摆法的比较中,体会摆出更多图形的关键在于重复使用小棒,积累相应的数学活动经验。
经历用小棒摆三角形和正方形的过程,体会不同摆法与所用小棒根数之间的关系,感受拼摆的乐趣。
实验准备
第46页中的小棒。
实验过程
1 摆摆数数
摆1个三角形要用3根小棒,摆2个三角形要用多少根小棒?

为什么用5根小棒也能摆出2个三角形?
2 想想摆摆
(1)用小棒摆3个三角形,可以怎样摆?最少要用多少根小棒?
(2)用11根小棒摆三角形,可以怎样摆?最多能摆出多少个同样的三角形?
3 摆摆比比
(1)摆4个同样的正方形,要用多少根小棒?


4 回顾反思
用小棒摆三角形或正方形,要想所用小棒的根数尽量少,你有什么好办法?
本实验可以在学习二年级上册“1~6的表内乘法”时进行。
“摆摆数数”是用小棒摆出2个三角形,感受不同摆法所用小棒的根数不一样。
“想想摆摆”继续用小棒摆三角形,先是摆出指定个数的三角形,接着用指定根数的小棒摆出尽量多的三角形,鼓励学生探索不同的摆法。
“摆摆比比”是用小棒摆正方形,在不同摆法的比较中,体会摆出更多图形的关键在于重复使用小棒,积累相应的数学活动经验。
答案:
1. 摆1个三角形要用3根小棒。
摆2个三角形,若分开摆,需要$3×2 = 6$根小棒;若共用一条边摆,需要$3+2 = 5$根小棒。
所以用5根小棒摆2个三角形是因为两个三角形共用了一条边。
2.
(1) 摆3个三角形:
若分开摆,需要$3×3 = 9$根小棒;
若每两个三角形共用一条边,最少需要$3 + 2×2=7$根小棒。
(2) 用11根小棒摆三角形:
因为每个三角形3根小棒,$11÷3 = 3\cdots\cdots2$,
所以最多能摆3个同样的三角形,剩下2根小棒不够摆一个三角形。
可以这样摆:先摆3个独立的三角形用9根小棒,剩下2根小棒可以和其中一个三角形共用一条边(摆法不唯一)。
3.
(1) 摆4个同样的正方形:
若分开摆,需要$4×4 = 16$根小棒;
若每两个正方形共用一条边,从左到右依次摆,第一个正方形用4根,后面每个正方形用3根,
则最少需要$4+3×3 = 13$根小棒;
若摆成2行2列,每行每列都共用边,则需要$2×4 + 2×3=12$根小棒。
(2) 用24根小棒摆正方形:
若摆成1行,$24÷4 = 6$,能摆6个正方形;
若摆成2行,设每行x个,则$4x+3(x - 1)×2 = 24$(这里$4x$是每行小棒数,$3(x - 1)×2$是共用的小棒数),
$4x + 6x-6 = 24$,
$10x=30$,
解得$x = 3$,一共能摆$2×3 = 6$个正方形;
若摆成3行,设每行x个,则$4x+3(x - 1)×4 = 24$,
$4x+12x - 12 = 24$,
$16x=36$,
$x$不是整数,不符合要求。
所以最多能摆6个同样的正方形。
4. 要想所用小棒的根数尽量少,应该让图形尽可能多地共用边。
摆2个三角形,若分开摆,需要$3×2 = 6$根小棒;若共用一条边摆,需要$3+2 = 5$根小棒。
所以用5根小棒摆2个三角形是因为两个三角形共用了一条边。
2.
(1) 摆3个三角形:
若分开摆,需要$3×3 = 9$根小棒;
若每两个三角形共用一条边,最少需要$3 + 2×2=7$根小棒。
(2) 用11根小棒摆三角形:
因为每个三角形3根小棒,$11÷3 = 3\cdots\cdots2$,
所以最多能摆3个同样的三角形,剩下2根小棒不够摆一个三角形。
可以这样摆:先摆3个独立的三角形用9根小棒,剩下2根小棒可以和其中一个三角形共用一条边(摆法不唯一)。
3.
(1) 摆4个同样的正方形:
若分开摆,需要$4×4 = 16$根小棒;
若每两个正方形共用一条边,从左到右依次摆,第一个正方形用4根,后面每个正方形用3根,
则最少需要$4+3×3 = 13$根小棒;
若摆成2行2列,每行每列都共用边,则需要$2×4 + 2×3=12$根小棒。
(2) 用24根小棒摆正方形:
若摆成1行,$24÷4 = 6$,能摆6个正方形;
若摆成2行,设每行x个,则$4x+3(x - 1)×2 = 24$(这里$4x$是每行小棒数,$3(x - 1)×2$是共用的小棒数),
$4x + 6x-6 = 24$,
$10x=30$,
解得$x = 3$,一共能摆$2×3 = 6$个正方形;
若摆成3行,设每行x个,则$4x+3(x - 1)×4 = 24$,
$4x+12x - 12 = 24$,
$16x=36$,
$x$不是整数,不符合要求。
所以最多能摆6个同样的正方形。
4. 要想所用小棒的根数尽量少,应该让图形尽可能多地共用边。
查看更多完整答案,请扫码查看


