《2025年状元成才路创优作业100分三年级数学上册人教版广东专版》

1 选一选。(将正确答案的序号填在括号里)
(1)(河源真题)如图的线读作(C)。

A.线段 AB
B.线段 BA
C.直线 AB
D.射线 AB

答案： C　

(2)下面的图形中线段条数最多的是(B)。

答案： B

(3)做操时,老师让同学们站成一条直线,要求同学们站好后目视前方只能看见前一名同学的后脑勺,老师这样做的依据是(A)。
A.过两点只能画一条直线
B.两点之间,线段最短
C.线段可以度量长度
D.直线可以无限延伸

答案： A

2 画一画,填一填。
(1)过点 O 画直线 m,然后在直线 m 上取一点 C,使线段 OC 长 3 厘米。经过点 O 可以画(无数)条直线。
(2)过 A、B 两点画直线 n,再用圆规在直线 n 上作线段 BD,使 BD = AB。

步骤一：用直尺过A、B两点画直线n。步骤二：用圆规量取AB的长度（将圆规的一脚放在A点，另一脚放在B点，确定圆规两脚间的距离为AB的长度）。步骤三：以B为端点，在直线n上，用圆规截取BD=AB（将圆规有针的一脚放在B点，另一脚在直线n上画弧，确定D点）。

答案： 1. 对于（1）：
解：根据直线的性质，经过一点可以画无数条直线。
所以经过点$O$可以画无数条直线。
2. 对于（2）：
步骤一：用直尺过$A$、$B$两点画直线$n$。
步骤二：用圆规量取$AB$的长度（将圆规的一脚放在$A$点，另一脚放在$B$点，确定圆规两脚间的距离为$AB$的长度）。
步骤三：以$B$为端点，在直线$n$上，用圆规截取$BD = AB$（将圆规有针的一脚放在$B$点，另一脚在直线$n$上画弧，确定$D$点）。
综上，（1）的答案是无数。

3 看一看,量一量,下面每组线段中的两条线段长度相等吗？(填“相等”或“不相等”)
(1) (相等)
(2) (相等)

答案：
(1)相等　
(2)相等

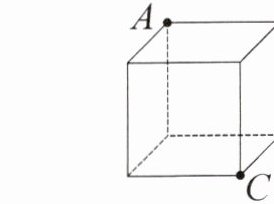
4 下图的正方体盒子上,一只蚂蚁要从点 A 爬到点 B,怎么爬最近？从点 A 爬到点 C 呢？在图中分别画一画。

答案：
(第二问画法不唯一)
[解析]因为两点间所有连线中线段最短，所以连接点A与点B就能得到A、B之间最短的路线。点A与点C不在盒子的同一个面上，可以先把盒子的两个面展开(如下图),再连接点A、点C两点就能得到A、C之间最短的路线，展开的两个面不同，得到的路线也不同。