第61页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
2. 把一个长方形框架拉成一个平行四边形框架后,这个平行四边形的周长和原来长方形的周长相比,(
A.不变
B.变大
C.变小
A
)。A.不变
B.变大
C.变小
答案:
A
3. 下面的图形中,(
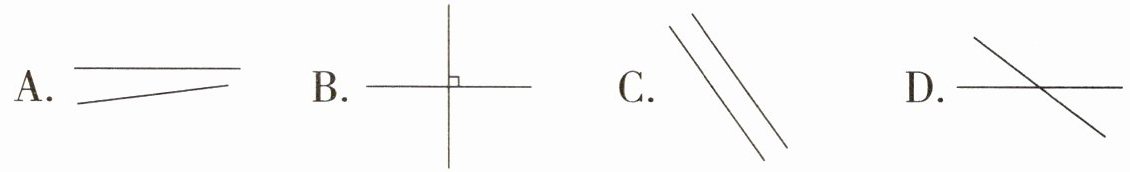
A.
B.
C.
D.
C
)是一组平行线,(B
)是一组互相垂直的线。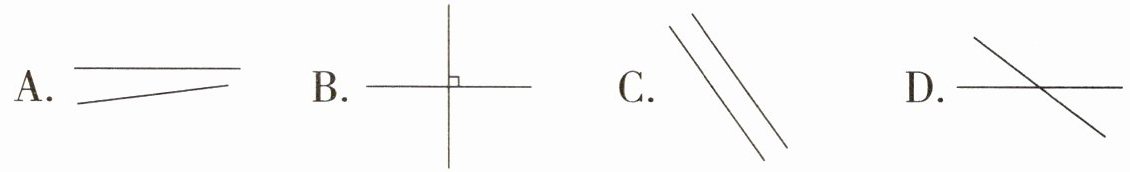
A.
B.
C.
D.
答案:
C B
1. 过点 $ A $ 画角的两边的垂线。


答案:
答:
(1) 准备工具:选择直角三角板;
(2) 定位点A:确定点A在角范围内的位置;
(3) 画第一条垂线:将直角三角板的一条直角边与角的一边重合,移动三角板使另一条直角边过点A,沿该直角边从点A向角的边画垂线,标垂足;
(4) 画第二条垂线:重复上一步骤,对角的另一边画垂线;
(5) 检查:确认两条垂线都从点A出发且与角的两边垂直相交。
(1) 准备工具:选择直角三角板;
(2) 定位点A:确定点A在角范围内的位置;
(3) 画第一条垂线:将直角三角板的一条直角边与角的一边重合,移动三角板使另一条直角边过点A,沿该直角边从点A向角的边画垂线,标垂足;
(4) 画第二条垂线:重复上一步骤,对角的另一边画垂线;
(5) 检查:确认两条垂线都从点A出发且与角的两边垂直相交。
2. 过点 $ P $ 画已知线段 $ AB $ 的平行线,再利用这一组平行线画一个最大的正方形。
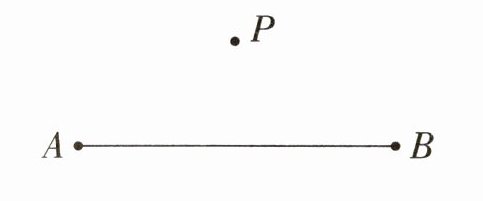
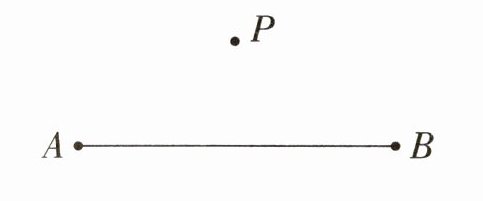
答案:
答题过程:
过点$P$画线段$AB$的平行线:
使用直尺对齐线段$AB$。
保持直尺不动,平移直尺至点$P$的位置。
沿着直尺,通过点$P$画一条与$AB$平行的直线,设为$l$。
利用平行线画最大的正方形:
选择线段$AB$上的一个点$Q$(假设$Q$为$AB$上离$P$垂直距离最近的点,或任意一点,实际操作中可能需要通过垂足来确定),使用直角三角板的一条直角边与线段$AB$重合。
保持直角三角板不动,平移直角三角板至点$P$处,使另一条直角边经过点$P$,与直线$l$相交于点$P$(这一步实际上是确认正方形的上边方向)。
从点$P$出发,沿着直角三角板的这条直角边画一条直线,与直线$l$(即平行于$AB$的线)形成正方形的上边,设交点为$C$($C$为新画的直线与$l$的交点)。
使用同样的方法,或者利用正方形的性质(四边等长,四个直角),从点$C$出发,画一条与线段$PQ$(或$AB$,因为$PQ$平行于$AB$)垂直且等长的线段,作为正方形的右边,设交点为$R$。
连接点$P$和点$R$,完成正方形的绘制。
由于题目要求最大的正方形,因此应确保正方形的边长等于点$P$到线段$AB$的垂直距离(即高),这样画出的正方形就是利用这组平行线能画出的最大正方形。
最终图形为一个正方形,其中一边在直线$l$上,与线段$AB$平行,且正方形的一个顶点为点$P$。
过点$P$画线段$AB$的平行线:
使用直尺对齐线段$AB$。
保持直尺不动,平移直尺至点$P$的位置。
沿着直尺,通过点$P$画一条与$AB$平行的直线,设为$l$。
利用平行线画最大的正方形:
选择线段$AB$上的一个点$Q$(假设$Q$为$AB$上离$P$垂直距离最近的点,或任意一点,实际操作中可能需要通过垂足来确定),使用直角三角板的一条直角边与线段$AB$重合。
保持直角三角板不动,平移直角三角板至点$P$处,使另一条直角边经过点$P$,与直线$l$相交于点$P$(这一步实际上是确认正方形的上边方向)。
从点$P$出发,沿着直角三角板的这条直角边画一条直线,与直线$l$(即平行于$AB$的线)形成正方形的上边,设交点为$C$($C$为新画的直线与$l$的交点)。
使用同样的方法,或者利用正方形的性质(四边等长,四个直角),从点$C$出发,画一条与线段$PQ$(或$AB$,因为$PQ$平行于$AB$)垂直且等长的线段,作为正方形的右边,设交点为$R$。
连接点$P$和点$R$,完成正方形的绘制。
由于题目要求最大的正方形,因此应确保正方形的边长等于点$P$到线段$AB$的垂直距离(即高),这样画出的正方形就是利用这组平行线能画出的最大正方形。
最终图形为一个正方形,其中一边在直线$l$上,与线段$AB$平行,且正方形的一个顶点为点$P$。
五、有一个等腰梯形上底长 $ 12 $ 米,下底长 $ 18 $ 米,一条腰长 $ 9 $ 米。这个梯形的周长是多少米?
答案:
12+18+9+9=48(米)
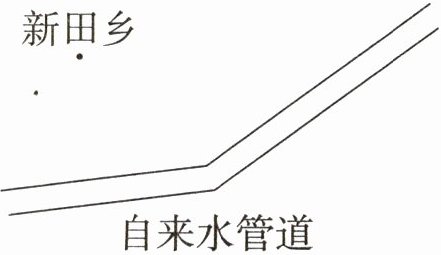
六、为了给新田乡接通自来水管道,从哪里接入最省材料?请画出来。

答案:
本题可根据“点到直线的距离中,垂线段最短”这一原理来确定从哪里接入最省材料。
- **步骤一:分析原理
根据数学知识,点到直线的距离中,垂线段最短。在本题中,新田乡可看作一个点,自来水管道可看作一条直线,要使接入的自来水管道最省材料,也就是要使新田乡到自来水管道的距离最短,那么就需要从新田乡向自来水管道作垂线段。
- **步骤二:作图
过新田乡的两个点分别向自来水管道作垂线段(由于无法直接为您画图,您可以使用三角板,将三角板的一条直角边与自来水管道重合,另一条直角边经过新田乡的点,沿着这条直角边画线段,就是垂线段),沿着垂线段接入最省材料。
综上,从新田乡向自来水管道作垂线段,沿着垂线段接入最省材料(具体图形需根据上述方法画出)。
- **步骤一:分析原理
根据数学知识,点到直线的距离中,垂线段最短。在本题中,新田乡可看作一个点,自来水管道可看作一条直线,要使接入的自来水管道最省材料,也就是要使新田乡到自来水管道的距离最短,那么就需要从新田乡向自来水管道作垂线段。
- **步骤二:作图
过新田乡的两个点分别向自来水管道作垂线段(由于无法直接为您画图,您可以使用三角板,将三角板的一条直角边与自来水管道重合,另一条直角边经过新田乡的点,沿着这条直角边画线段,就是垂线段),沿着垂线段接入最省材料。
综上,从新田乡向自来水管道作垂线段,沿着垂线段接入最省材料(具体图形需根据上述方法画出)。
查看更多完整答案,请扫码查看


