《2025年云南师大附小一线名师提优作业四年级数学上册人教版》

1. 要准确测量一个角的大小,可以用(量角器)来测量。

答案： 量角器

2. 人们将圆平均分成360份,将其中1份所对的角作为度量(角)的单位,它的大小就是1度,记作(1°)。

答案： 角 1°

3. 量角时要把量角器的中心与角的(顶点)重合,$0^{\circ}$刻度线与角的一条边(重合)。角的另一边所对的量角器上的(刻度),就是这个角的(度数)。

答案： 顶点 重合 刻度 度数

二、下面图形是角的在( )里打“√”。

第一个、第四个

答案： 第一个、第四个

三、先估一估,再量出下图中各角的度数。

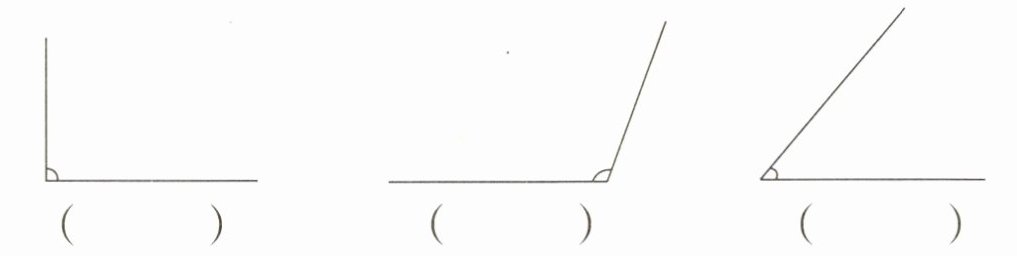
答案： 1. 首先进行估算：
第一个角：看起来接近直角，可估算为$90^{\circ}$。
第二个角：比直角大，可估算为$120^{\circ}$。
第三个角：比直角小，可估算为$30^{\circ}$。
2. 然后用量角器测量（测量方法：把量角器的中心与角的顶点重合，$0^{\circ}$刻度线与角的一条边重合，角的另一条边所对的量角器上的刻度，就是这个角的度数）：
第一个角：$90^{\circ}$。
第二个角：$120^{\circ}$。
第三个角：$30^{\circ}$。
答案依次为$90^{\circ}$；$120^{\circ}$；$30^{\circ}$。

四、先估计三角尺上各角的度数,再量一量。

$\angle 1 = $(60°)
$\angle 2 = $(90°)
$\angle 2 = $(30°)
$\angle 3 = $(45°)
$\angle 3 = $(90°)

答案： 60° 90° 30° 45° 90° 45°