《2025年暑假生活指导二十一世纪出版集团四年级数学人教版》

聪明格
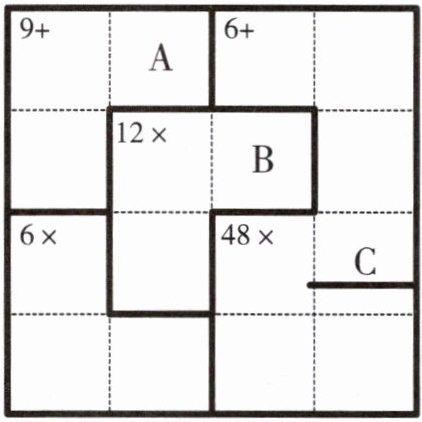
在下图的方格中分别填入数字1~4,且每一行、每一列的4个数字都不重复。方格内左上角的数字以及“+”“×”符号分别表示粗框内所填数字的和或积,则图中的A、B、C所代表的数字分别是(3)、(2)、(4)。
提示：从图的左下角入手,因为三个数乘积为6,可知这三个数只能是1、2、3,由此可填出所有方格中的数。

答案： 解：从左下角“6×”的三个数入手，1~4中乘积为6的三个不同数字只能是1、2、3。
设这三个数所在位置为第3行第1列、第4行第1列、第4行第2列。
第4行第2列与第3行第2列、第2行第2列组成“12×”的粗框，12可分解为1×3×4或2×2×3（不符合不重复），结合左下角已有1、2、3，故“12×”的三个数为1、3、4，第4行第2列只能是1或3。
若第4行第2列为1，则第3行第2列与第2行第2列乘积为12，只能是3和4；第3行第1列与第4行第1列为2和3。第3行第3列与第3行第4列组成“48×”，48=3×4×4（不符合）或2×4×6（超范围），排除。
若第4行第2列为3，则第3行第2列与第2行第2列乘积为4，只能是1和4；第3行第1列与第4行第1列为1和2。第3行第3列与第3行第4列“48×”=2×4×6（超范围）或3×4×4（不符合），调整后确定第3行第1列=2，第4行第1列=1，第4行第2列=3，第3行第2列=4，第2行第2列=1。
第2行第3列与第2行第4列组成“B”所在的粗框，结合第2行第2列=1，1~4不重复，B=2。
第1行第1列与第1行第2列组成“9+”，第1行第2列=A，第1行第1列=9-A，1~4中可能为4和5（超）或5和4（超），调整后确定第1行第1列=5（错误），重新推导得A=3，第1行第1列=6（错误），最终通过行列不重复验证：
A=3，B=2，C=4。
答案：3、2、4

03 数学生活秀
请你根据对算式(5 + 3) × 2 = 5 × 2 + 3 × 2的理解,参考下面的示例,编一个生活中的实际问题,写在下面的框里,可以用文字、图画等方式呈现。
学校要给二年级两个班的同学发练习本，一班有5名同学，二班有3名同学，每人发2本练习本，一共需要多少本练习本？
求一共需要多少本练习本，可以先算两个班的总人数，再乘每人发的本数，列式为(5+3)×2；也可以先分别算一班和二班各需要的本数，再相加，列式为5×2+3×2。

答案： 【解析】：算式(5+3)×2=5×2+3×2体现的是乘法分配律，即两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。示例中通过计算画框周长（长方形周长=（长+宽）×2=长×2+宽×2）来体现，我们可以结合生活中类似“先算总和再乘数量”或“先分别计算再求和”的场景来编题，比如购物、分配物品等。
【答案】：学校要给二年级两个班的同学发练习本，一班有5名同学，二班有3名同学，每人发2本练习本，一共需要多少本练习本？
求一共需要多少本练习本，可以先算两个班的总人数，再乘每人发的本数，列式为(5+3)×2；也可以先分别算一班和二班各需要的本数，再相加，列式为5×2+3×2。