《2025年课时提优计划作业本七年级数学上册苏科版》

1. 某人以 $6 \mathrm{~km} / \mathrm{h}$ 的速度在 $400 \mathrm{~m}$ 的环形跑道上行走, 他从 $A$ 处出发, 按顺时针方向走了 $1 \mathrm{~min}$, 再按逆时针方向走了 $3 \mathrm{~min}$, 然后又按顺时针方向走 $5 \mathrm{~min}$, 这时他想回到出发点 $A$ 处, 最少需要的时间为 ( )

A.$3 \mathrm{~min}$
B.$5 \mathrm{~min}$
C.$2 \mathrm{~min}$
D.$1 \mathrm{~min}$

答案： D 解析:6 km/h=100 m/min,设 A 为原点,按顺时针方向走记为正,按逆时针方向走记为负,则他此时离出发点的距离为[1+(-3)+5]×100=300(m).因为环形跑道长为400 m,所以回到原点的最短距离为400-300=100(m),所以需要的时间为100÷100=1(min).

2. 小明、小杰两人在环形跑道上练习跑步, 已知环形跑道一圈长 $420 \mathrm{~m}$, 小杰每秒钟跑 $6 \mathrm{~m}$, 小明的速度是小杰的速度的 $1 \frac{1}{3}$ 倍, 如果小明、小杰在跑道上同一地点同时反向出发. 问:
(1) 经过多长时间两人首次相遇?
(2) 第二次相遇时与出发点相距多远?
(3) 若他们继续跑下去, 他们有可能在出发点相遇吗? 若有可能, 说出一种可能的情况; 若不可能, 请说明理由.

答案：
(1)设 x s后两人首次相遇,则有$6x+6×\frac {4}{3}x=420$,解得x=30.答:经过30 s两人首次相遇.
(2)由
(1)知,经过30 s两人首次相遇,所以经过60 s,两人第二次相遇,这时小明一共跑了$60×6×\frac {4}{3}=480(m),480-420=60(m)$.答:第二次相遇时与出发点相距60 m.
(3)有可能在出发点相遇.如当小杰跑6圈,小明跑8圈时他们会在出发点相遇,或在420 s时会在出发点相遇,或第14次相遇在出发点.

3. 已知甲、乙两人在一个 $200 \mathrm{~m}$ 的环形跑道上练习跑步, 现在把跑道分成相等的 4 段, 即两条直道和两条弯道的长度相等. 甲平均每秒跑 $4 \mathrm{~m}$, 乙平均每秒跑 $6 \mathrm{~m}$, 若甲、乙两人分别从 $A 、 C$ 两处同时相向出发 (如图), 则:
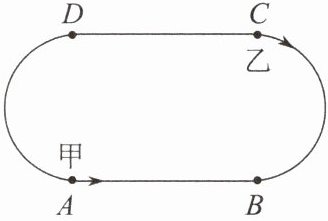
(1) 多长时间后两人首次相遇? 请说出此时他们在跑道上的具体位置.
(2) 首次相遇后, 又经过多长时间他们再次相遇?
(3) 他们第 100 次相遇时,在哪一条段跑道上?

答案：
(1)设x s后两人首次相遇.根据题意,得4x+6x=100,解得x=10,所以甲跑的路程为4×10=40(m),200÷4-40=10(m).答:10 s后两人首次相遇,此时他们在直道 AB上,且到点 B 的距离为10 m.
(2)设又经过y s两人再次相遇.根据题意,得4y+6y=200,解得y=20.答:首次相遇后,又经过20 s两人再次相遇.
(3)第1次相遇,总共用时10 s;第2次相遇,总用时10+20×1,即30 s;第3次相遇,总用时10+20×2,即50 s;第100次相遇,总用时10+20×99,即1 990 s,此时甲跑的圈数为1 990×4÷200=39.8,200×0.8=160(m),此时他们在弯道 AD上.