例1 如图,EF与DC互相平行,平行四边形ABCD的面积是58平方厘米,则图中涂色部分的面积是多少平方厘米?
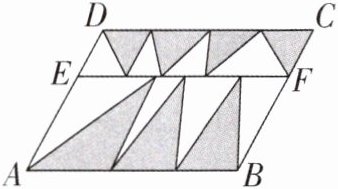
[解析]设上面四个涂色三角形的底分别为$a_{1}$、$a_{2}$、$a_{3}$、$a_{4}$,下面三个涂色三角形的底分别为$a_{5}$、$a_{6}$、$a_{7}$,上、下两组三角形的高分别为$h_{1}$、$h_{2}$,平行四边形ABCD的底为a,高为h,则涂色三角形的面积和为$a_{1}×h_{1}÷2+a_{2}×h_{1}÷2+a_{3}×h_{1}÷2+a_{4}×h_{1}÷2+a_{5}×h_{2}÷2+a_{6}×h_{2}÷2+a_{7}×h_{2}÷2= (a_{1}+a_{2}+a_{3}+a_{4})×h_{1}÷2+(a_{5}+a_{6}+a_{7})×h_{2}÷2= a×h_{1}÷2+a×h_{2}÷2= a×(h_{1}+h_{2})÷2= a×h÷2$,即涂色部分的面积是平行四边形面积的一半。
[答案]$58÷2= 29$(平方厘米)
答:图中涂色部分的面积是29平方厘米。
点评:先将高相等且分散的三角形整合成两个三角形,再整合成一个三角形。利用乘法分配律不仅可以进行简便计算,还可以探究图形面积之间的关系。

[解析]设上面四个涂色三角形的底分别为$a_{1}$、$a_{2}$、$a_{3}$、$a_{4}$,下面三个涂色三角形的底分别为$a_{5}$、$a_{6}$、$a_{7}$,上、下两组三角形的高分别为$h_{1}$、$h_{2}$,平行四边形ABCD的底为a,高为h,则涂色三角形的面积和为$a_{1}×h_{1}÷2+a_{2}×h_{1}÷2+a_{3}×h_{1}÷2+a_{4}×h_{1}÷2+a_{5}×h_{2}÷2+a_{6}×h_{2}÷2+a_{7}×h_{2}÷2= (a_{1}+a_{2}+a_{3}+a_{4})×h_{1}÷2+(a_{5}+a_{6}+a_{7})×h_{2}÷2= a×h_{1}÷2+a×h_{2}÷2= a×(h_{1}+h_{2})÷2= a×h÷2$,即涂色部分的面积是平行四边形面积的一半。
[答案]$58÷2= 29$(平方厘米)
答:图中涂色部分的面积是29平方厘米。
点评:先将高相等且分散的三角形整合成两个三角形,再整合成一个三角形。利用乘法分配律不仅可以进行简便计算,还可以探究图形面积之间的关系。
答案:
设上面四个涂色三角形的底分别为$a_{1}$、$a_{2}$、$a_{3}$、$a_{4}$,下面三个涂色三角形的底分别为$a_{5}$、$a_{6}$、$a_{7}$,上、下两组三角形的高分别为$h_{1}$、$h_{2}$,平行四边形$ABCD$的底为$a$,高为$h$。
涂色三角形面积和为:
$\begin{aligned}&a_{1}h_{1}÷2 + a_{2}h_{1}÷2 + a_{3}h_{1}÷2 + a_{4}h_{1}÷2 + a_{5}h_{2}÷2 + a_{6}h_{2}÷2 + a_{7}h_{2}÷2\\=&(a_{1}+a_{2}+a_{3}+a_{4})h_{1}÷2 + (a_{5}+a_{6}+a_{7})h_{2}÷2\\=&ah_{1}÷2 + ah_{2}÷2\\=&a(h_{1}+h_{2})÷2\\=&ah÷2\end{aligned}$
因为平行四边形$ABCD$面积为$ah = 58$平方厘米,所以涂色部分面积为$58÷2 = 29$平方厘米。
答:图中涂色部分的面积是29平方厘米。
涂色三角形面积和为:
$\begin{aligned}&a_{1}h_{1}÷2 + a_{2}h_{1}÷2 + a_{3}h_{1}÷2 + a_{4}h_{1}÷2 + a_{5}h_{2}÷2 + a_{6}h_{2}÷2 + a_{7}h_{2}÷2\\=&(a_{1}+a_{2}+a_{3}+a_{4})h_{1}÷2 + (a_{5}+a_{6}+a_{7})h_{2}÷2\\=&ah_{1}÷2 + ah_{2}÷2\\=&a(h_{1}+h_{2})÷2\\=&ah÷2\end{aligned}$
因为平行四边形$ABCD$面积为$ah = 58$平方厘米,所以涂色部分面积为$58÷2 = 29$平方厘米。
答:图中涂色部分的面积是29平方厘米。
1. 如图,平行四边形ABCD的底是10厘米,高是4厘米,线段EF、AD互相平行,则平行四边形内涂色部分的面积是多少?
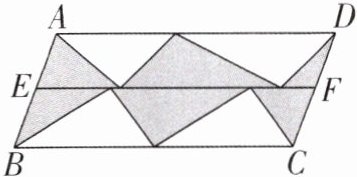

答案:
10×4÷2=20(平方厘米) 解析:观察题图可知,四边形ADFE是一个平行四边形,它内部涂色的三个三角形的高相等,不妨从左到右设这三个三角形的底分别是a、b、c,高是$h_{1}$,那么这三个三角形的面积之和是$a× h_{1}÷2 + b× h_{1}÷2 + c× h_{1}÷2=(a + b + c)× h_{1}÷2$。因为EF的长是$(a + b + c)$,所以这三个三角形的面积之和是$EF× h_{1}÷2$,且$EF× h_{1}÷2$恰好是平行四边形ADFE面积的一半。同理,四边形BCFE也是平行四边形,它内部涂色的三个三角形的面积之和也是它面积的一半。所以涂色部分的面积是平行四边形ABCD面积的一半。
例2 如图,P是边长为12厘米的正方形ABCD内任意一点,E、F、G、H分别是AD、BC的三等分点。I、J分别是AB、CD的中点,并连接点P与各点。求涂色部分的面积。

[解析]由E、F、G、H分别是AD、BC的三等分点可得,$EF= HG= 12÷3= 4$(厘米)。设三角形EFP和三角形HPG的高分别为$h_{1}$、$h_{2}$,则左、右两个涂色三角形的面积和为$4×h_{1}÷2+4×h_{2}÷2= 4×(h_{1}+h_{2})÷2= 4×12÷2= 24$(平方厘米)。同理,上、下两个涂色三角形的面积和为$12÷2×12÷2= 36$(平方厘米),所以涂色部分的面积为$24+36= 60$(平方厘米)。
[答案]$12÷3= 4$(厘米)$12÷2= 6$(厘米)$4×12÷2+6×12÷2= 60$(平方厘米)
答:涂色部分的面积是60平方厘米。
点评:巧用乘法分配律可以将未知条件转化为已知条件,进而求解。

[解析]由E、F、G、H分别是AD、BC的三等分点可得,$EF= HG= 12÷3= 4$(厘米)。设三角形EFP和三角形HPG的高分别为$h_{1}$、$h_{2}$,则左、右两个涂色三角形的面积和为$4×h_{1}÷2+4×h_{2}÷2= 4×(h_{1}+h_{2})÷2= 4×12÷2= 24$(平方厘米)。同理,上、下两个涂色三角形的面积和为$12÷2×12÷2= 36$(平方厘米),所以涂色部分的面积为$24+36= 60$(平方厘米)。
[答案]$12÷3= 4$(厘米)$12÷2= 6$(厘米)$4×12÷2+6×12÷2= 60$(平方厘米)
答:涂色部分的面积是60平方厘米。
点评:巧用乘法分配律可以将未知条件转化为已知条件,进而求解。
答案:
解析:
本题可通过分析图形中各部分之间的关系,利用乘法分配律来求解涂色部分的面积。
已知正方形边长为$12$厘米,E、F、G、H分别是AD、BC的三等分点,则$EF = HG = 12÷3 = 4$厘米;I、J分别是AB、CD的中点,则$AI = IB = DJ = JC = 12÷2 = 6$厘米。
设$\triangle EFP$和$\triangle HPG$的高分别为$h_1$、$h_2$,由于正方形ABCD的边长为$12$厘米,即$h_1 + h_2 = 12$厘米。
根据三角形面积公式$S = \frac{1}{2}ah$(其中$a$为底,$h$为高),可得左、右两个涂色三角形($\triangle EFP$和$\triangle HPG$)的面积和为:
$S_{\triangle EFP}+S_{\triangle HPG}=\frac{1}{2}× EF× h_1+\frac{1}{2}× HG× h_2=\frac{1}{2}×4× h_1+\frac{1}{2}×4× h_2 = 4×\frac{h_1 + h_2}{2}=4×12÷2 = 24$(平方厘米)。
同理,设$\triangle AIP$和$\triangle DJP$的高分别为$h_3$、$h_4$,则$h_3 + h_4 = 12$厘米,上、下两个涂色三角形($\triangle AIP$和$\triangle DJP$)的面积和为:
$S_{\triangle AIP}+S_{\triangle DJP}=\frac{1}{2}× AI× h_3+\frac{1}{2}× DJ× h_4=\frac{1}{2}×6× h_3+\frac{1}{2}×6× h_4 = 6×\frac{h_3 + h_4}{2}=6×12÷2 = 36$(平方厘米)。
将左、右两个涂色三角形的面积和与上、下两个涂色三角形的面积和相加,可得涂色部分的面积为:
$S = 24 + 36 = 60$(平方厘米)。
答案:
$12÷3 = 4$(厘米)
$12÷2 = 6$(厘米)
$4×12÷2 + 6×12÷2 = 60$(平方厘米)
答:涂色部分的面积是60平方厘米。
本题可通过分析图形中各部分之间的关系,利用乘法分配律来求解涂色部分的面积。
已知正方形边长为$12$厘米,E、F、G、H分别是AD、BC的三等分点,则$EF = HG = 12÷3 = 4$厘米;I、J分别是AB、CD的中点,则$AI = IB = DJ = JC = 12÷2 = 6$厘米。
设$\triangle EFP$和$\triangle HPG$的高分别为$h_1$、$h_2$,由于正方形ABCD的边长为$12$厘米,即$h_1 + h_2 = 12$厘米。
根据三角形面积公式$S = \frac{1}{2}ah$(其中$a$为底,$h$为高),可得左、右两个涂色三角形($\triangle EFP$和$\triangle HPG$)的面积和为:
$S_{\triangle EFP}+S_{\triangle HPG}=\frac{1}{2}× EF× h_1+\frac{1}{2}× HG× h_2=\frac{1}{2}×4× h_1+\frac{1}{2}×4× h_2 = 4×\frac{h_1 + h_2}{2}=4×12÷2 = 24$(平方厘米)。
同理,设$\triangle AIP$和$\triangle DJP$的高分别为$h_3$、$h_4$,则$h_3 + h_4 = 12$厘米,上、下两个涂色三角形($\triangle AIP$和$\triangle DJP$)的面积和为:
$S_{\triangle AIP}+S_{\triangle DJP}=\frac{1}{2}× AI× h_3+\frac{1}{2}× DJ× h_4=\frac{1}{2}×6× h_3+\frac{1}{2}×6× h_4 = 6×\frac{h_3 + h_4}{2}=6×12÷2 = 36$(平方厘米)。
将左、右两个涂色三角形的面积和与上、下两个涂色三角形的面积和相加,可得涂色部分的面积为:
$S = 24 + 36 = 60$(平方厘米)。
答案:
$12÷3 = 4$(厘米)
$12÷2 = 6$(厘米)
$4×12÷2 + 6×12÷2 = 60$(平方厘米)
答:涂色部分的面积是60平方厘米。
2. 如图,三角形的周长是34厘米,三角形内一点P到三角形三条边的距离都是3厘米,求三角形的面积。
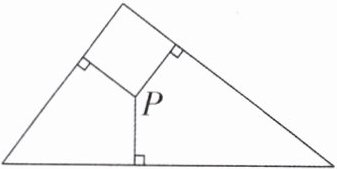

答案:
34×3÷2=51(平方厘米) 解析:如图,连接点P与三角形的三个顶点,则原三角形被分成三个三角形,将原三角形的三条边分别记为$a_{1}$、$a_{2}$、$a_{3}$,则原三角形的面积是$a_{1}×3÷2 + a_{2}×3÷2 + a_{3}×3÷2=(a_{1}+a_{2}+a_{3})×3÷2$。因为$(a_{1}+a_{2}+a_{3})$等于原三角形的周长,所以原三角形的面积是34×3÷2=51(平方厘米)。
34×3÷2=51(平方厘米) 解析:如图,连接点P与三角形的三个顶点,则原三角形被分成三个三角形,将原三角形的三条边分别记为$a_{1}$、$a_{2}$、$a_{3}$,则原三角形的面积是$a_{1}×3÷2 + a_{2}×3÷2 + a_{3}×3÷2=(a_{1}+a_{2}+a_{3})×3÷2$。因为$(a_{1}+a_{2}+a_{3})$等于原三角形的周长,所以原三角形的面积是34×3÷2=51(平方厘米)。

查看更多完整答案,请扫码查看


