《2025年华东师大版一课一练四年级数学上册沪教版五四制增强版》

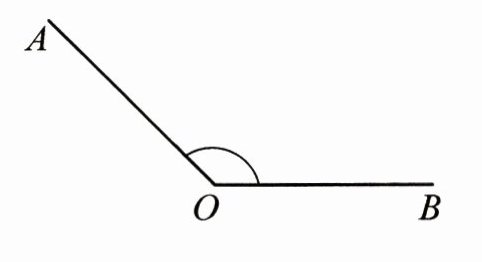
五、用量角器量下面的角


26
∠AOB= ( )

答案： 135°

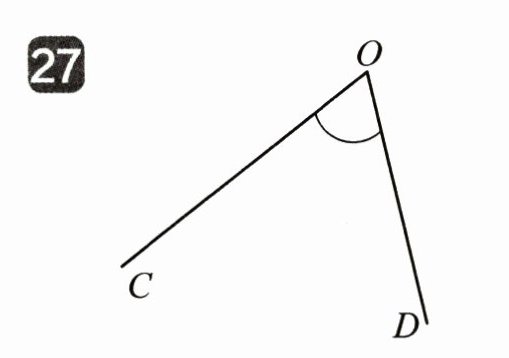
27
∠COD= ( )

答案： 解析：本题主要考查角的度量的相关知识点以及角的计算。
在几何题目中，如果没有给出具体的图形或足够的条件来确定$\angle COD$的度数，那么通常无法直接给出答案。
由于题目没有给出足够的信息来确定$\angle COD$的确切度数，且题目要求按照四年级学生的思维方式来解答，因此在此情况下，学生无法直接计算出$\angle COD$的度数。
答案：由于缺乏具体信息，无法确定$\angle COD$的度数。

六、画一画
28 用量角器画角,使∠BCD= 25°,∠AOB= 165°,∠AOC= 200°。

答案： 答案略

29 在下图的射线OA上：
(1)画一个以A为圆心,AB为半径的圆；
(2)画∠AOC= 120°。

答案： 解析：本题主要考查圆的画法以及角的画法。
(1) 圆的画法：
确定圆心A和半径AB。
使用圆规，将圆规的一脚放在点A上，另一脚调整到与点B的距离（即半径AB的长度）。
保持圆规的张开距离不变，将圆规旋转一周，画出以A为圆心，AB为半径的圆。
(2) 角的画法：
使用量角器或直尺和圆规来画出$\angle AOC = 120^\circ$。
如果没有量角器，可以使用直尺和圆规通过构造等边三角形和辅助线来画出$120^\circ$的角。
一个简单的方法是：在OA上取一点D，使得$AD = AB$，然后以D为圆心，DB为半径画弧，与OA的反向延长线交于点C。
由于$\triangle ADB$是等边三角形（因为$AD = AB$且$\angle DAB = 60^\circ$的补角情况，但在这里直接构造$120^\circ$更直观），
所以$\angle DBA = 60^\circ$，
那么$\angle AOC = 180^\circ - 60^\circ = 120^\circ$（因为OC是OA的反向延长线与弧的交点）。
但更直接且准确的方法是使用量角器：将量角器的中心对准点A，一条0刻度线对准OA，然后在量角器上找到$120^\circ$的刻度，连接点A与该刻度对应的点，即为射线OC。
答案：
(1) 图略（以A为圆心，AB为半径的圆）。
(2) 图略（$\angle AOC = 120^\circ$）。