第39页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
8.(2024·温州鹿城二模)小实在家利用甲、乙两个衣架组装成滑轮组进行实验。如图所示,小实将重为3牛的矿泉水瓶匀速提升0.5米。(不考虑衣架、绳子的自重和摩擦)下列说法正确的是(

A.甲相当于定滑轮,可以省力
B.乙相当于动滑轮,可以改变力的方向
C.自由端绳子通过的距离为2.5米
D.拉力的大小是0.5牛
]
C
)
A.甲相当于定滑轮,可以省力
B.乙相当于动滑轮,可以改变力的方向
C.自由端绳子通过的距离为2.5米
D.拉力的大小是0.5牛
]
答案:
C
9.(科技民生)(2024·宁波镇海期中)如图所示是高空修剪树枝的工具——高枝剪。当树枝进入两剪片形成的刀口中,拉动拉绳就能轻松剪断树枝。为了剪断较粗较硬的枝条,除了增大拉力外,还应尽量将枝条靠近______
]

O点
(填“A点”或“O点”)。若不计绳重、滑轮自重及摩擦,当用80N的拉力作用在绳子自由端时,B点受到绳子a的拉力为______240
N。]

答案:
O点;240
10. 在探究动滑轮使用特点的实验中,各小组按照图(a)所示进行实验,每个小组的实验器材都相同,每次都匀速提起钩码,实验中不计绳重和摩擦。
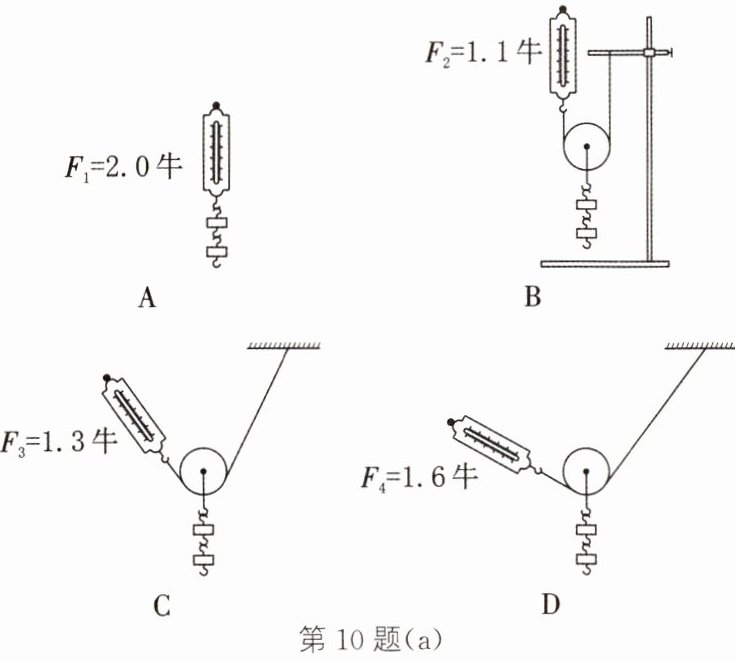
(1)由所学知识我们知道:使用动滑轮可以省一半的力,根据A,B两图求出他们所用动滑轮的重力为
(2)比较B、C、D三图可知,使用动滑轮匀速提起同一重物时拉力大小不同,原因
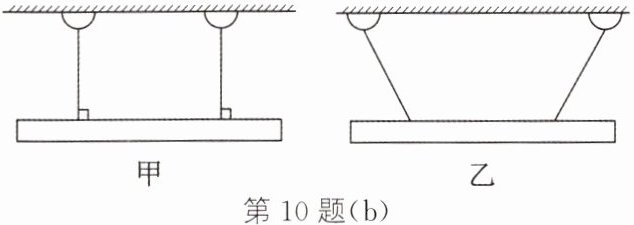
(3)根据实验,家里安装日光灯,图(b)更合理
]

(1)由所学知识我们知道:使用动滑轮可以省一半的力,根据A,B两图求出他们所用动滑轮的重力为
0.2
牛。 (2)比较B、C、D三图可知,使用动滑轮匀速提起同一重物时拉力大小不同,原因
拉力与竖直方向的夹角不同
。 (3)根据实验,家里安装日光灯,图(b)更合理
甲
。]

答案:
(1)0.2
(2)拉力与竖直方向的夹角不同
(3)甲
(1)0.2
(2)拉力与竖直方向的夹角不同
(3)甲
11.反思学习品质。"动滑轮"实验中小宁装置实验,结论:使用动滑轮匀速提升物体,竖直向上拉力F小于物重G。小宁认为,即使不计摩擦绳重,结论成立,物重G动滑轮重G动间满足条件。写出条件,证明。
]

]

答案:
条件:物重$G$大于动滑轮重$G_{动}$;证明:使用动滑轮匀速提升物体时,若不计摩擦和绳重,则竖直向上的拉力$F=\frac{1}{2}(G + G_{动})$,若$F<G$,即$\frac{1}{2}(G + G_{动})<G$,则$G>G_{动}$
12.如图所示,底面积$S= 1000cm^2、$高h= 2.1m圆柱形容器盛水,水面高度H= 18m。水中棱长0cm立方体物块(图未按比例画),物块密度ρ物= 。开始时,物块在滑轮组(不计摩擦及绳子滑轮重力)作用下静止水中,下表面与容器底面未接触,现拉着物块以v= 0.2m/s速度匀速上升10s。图中各绳子不会被拉断,物块匀速上升过程中,拉力F最大值最小值分别多少?(不计水阻力,g= 取N/kg,ρ水= )。
]

]

答案:
立方体物块体积$V = a^{3}=(0.1m)^{3}=1×10^{-3}m^{3}$,物块重力$G_{物}=m_{物}g=\rho_{物}Vg = 2.5×10^{3}kg/m^{3}×1×10^{-3}m^{3}×10N/kg = 25N$,该物块浸没在水中时受到的浮力$F_{浮}=\rho_{水}gV_{排}=\rho_{水}gV = 1.0×10^{3}kg/m^{3}×10N/kg×1×10^{-3}m^{3}=10N$,拉着物块以$v = 0.2m/s$的速度匀速上升$10s$,则物块在$10s$内上升的高度$h = vt = 0.2m/s×10s = 2m$,由于水面高度$H = 1.8m$,立方体物块棱长为$10cm$,以物块底部所处位置为标准,当物块提升$2m$时已从水中离开至水面上,由图可知绳子股数$n = 2$,则物块在水中时,$F_{最小}=\frac{G_{物}-F_{浮}}{n}=\frac{25N - 10N}{2}=7.5N$,物块离开水面后,$F_{最大}=\frac{G_{物}}{n}=\frac{25N}{2}=12.5N$
查看更多完整答案,请扫码查看


