《2025年阳光假日暑假三年级数学人教版》

4. 用 3 个相同的正方形排成一排拼成一个长方形,下面说法正确的是(C)。
A. 周长、面积都不变
B. 周长不变,面积变小
C. 周长变小,面积不变
D. 周长变大,面积不变

答案： C

五、如图所示为一面破损的墙面。

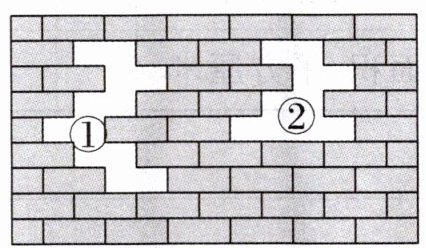
比一比,这两个墙洞(①)的面积大。

答案： 【解析】：可以通过数每个墙洞缺少的砖块数量来比较面积大小。假设每块砖面积相同，墙洞①缺少$6$块砖，墙洞②缺少$5$块砖。
【答案】：①

六、请你在下面画出面积是 1 平方厘米的正方形。

答案：

七、下面各图形是用面积为 1 平方分米的正方形拼成的。它们的周长各是多少分米? 面积各是多少平方分米?

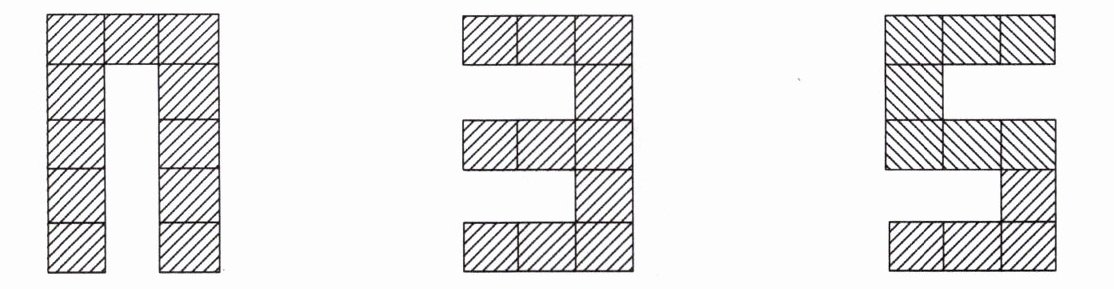
周长:(20)分米 (16)分米 (16)分米
面积:(12)平方分米 (10)平方分米 (11)平方分米

答案： 【解析】：
对于第一个图形（类似“n”）：
周长：通过平移法，可将其周长转化为一个长$5$分米、宽$3$分米的长方形周长加上$2$个$2$分米（缺口处）。长方形周长公式$C=(a + b)\times2$，$(5 + 3)\times2+2\times2=16 + 4=20$（分米）；面积：数小正方形个数，共$12$个，面积$1\times12 = 12$（平方分米）。
对于第二个图形（类似“3”）：
周长：通过平移法，可转化为一个长$5$分米、宽$3$分米的长方形周长，$(5 + 3)\times2=16$（分米）；面积：数小正方形个数，共$10$个，面积$1\times10 = 10$（平方分米）。
对于第三个图形（类似“5”）：
周长：通过平移法，可转化为一个长$5$分米、宽$3$分米的长方形周长，$(5 + 3)\times2=16$（分米）；面积：数小正方形个数，共$11$个，面积$1\times11 = 11$（平方分米）。
【答案】：
周长：$20$、$16$、$16$
面积：$12$、$10$、$11$