第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
七、根据提示,完成教室里的座位图。
1. 君君的西面是青青。
2. 明明和小叶都坐在小兰的东面,小叶坐在明明的西面。
3. 阳阳坐在小叶的南面,明明的北面是慧慧。
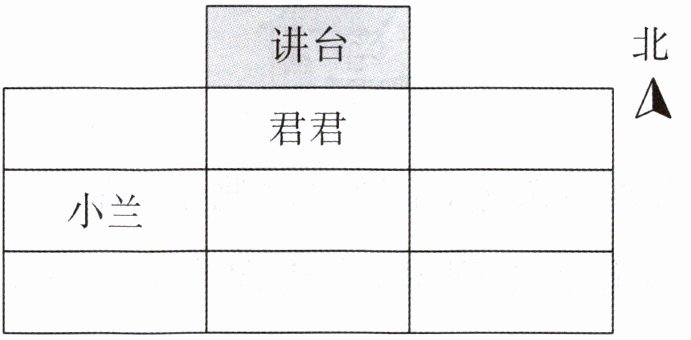
第一行:
第二行:
第三行:
1. 君君的西面是青青。
2. 明明和小叶都坐在小兰的东面,小叶坐在明明的西面。
3. 阳阳坐在小叶的南面,明明的北面是慧慧。

第一行:
青青
君君
慧慧
第二行:
小兰
小叶
明明
第三行:
阳阳
答案:
【解析】:根据“上北下南,左西右东”的方向原则,结合题目所给条件进行推理。
1. 因为君君的西面是青青,所以青青在君君左边。
2. 明明和小叶都坐在小兰的东面,小叶坐在明明的西面,所以从西到东依次是小兰、小叶、明明。
3. 阳阳坐在小叶的南面,即小叶下方是阳阳;明明的北面是慧慧,即明明上方是慧慧。
【答案】:
第一行:青青 君君 慧慧
第二行:小兰 小叶 明明
第三行:空 阳阳 空
1. 因为君君的西面是青青,所以青青在君君左边。
2. 明明和小叶都坐在小兰的东面,小叶坐在明明的西面,所以从西到东依次是小兰、小叶、明明。
3. 阳阳坐在小叶的南面,即小叶下方是阳阳;明明的北面是慧慧,即明明上方是慧慧。
【答案】:
第一行:青青 君君 慧慧
第二行:小兰 小叶 明明
第三行:空 阳阳 空
已知$\triangle ◯ □$是三个不同的数,并且$\triangle +\triangle +\triangle =◯ +◯$,$◯ +◯ +◯ +◯ =□ +□ +□$,$\triangle +◯ +◯ +□ =60$,那么,$\triangle +◯ +□$等于
45
。
答案:
【解析】:
1. 首先,根据已知条件进行等量代换:
已知$\triangle+\triangle+\triangle = \bigcirc+\bigcirc$,那么$4$个$\bigcirc$就等于$6$个$\triangle$(因为$4\bigcirc = 2\times(2\bigcirc)$,而$2\bigcirc = 3\triangle$,所以$4\bigcirc=6\triangle$)。
又因为$\bigcirc+\bigcirc+\bigcirc+\bigcirc=\square+\square+\square$,所以$\square+\square+\square = 6\triangle$,则$\square = 2\triangle$。
再由$\triangle+\triangle+\triangle=\bigcirc+\bigcirc$可得$\bigcirc=\frac{3}{2}\triangle$。
2. 然后,将$\bigcirc=\frac{3}{2}\triangle$和$\square = 2\triangle$代入$\triangle+\bigcirc+\bigcirc+\square = 60$中:
得到$\triangle+\frac{3}{2}\triangle+\frac{3}{2}\triangle + 2\triangle=60$。
对等式左边进行合并同类项:$(1 + \frac{3}{2}+\frac{3}{2}+2)\triangle=(1 + 3+2)\triangle=6\triangle$。
即$6\triangle = 60$,解得$\triangle = 10$。
3. 接着,求出$\bigcirc$和$\square$的值:
因为$\bigcirc=\frac{3}{2}\triangle$,$\triangle = 10$,所以$\bigcirc=\frac{3}{2}\times10 = 15$。
因为$\square = 2\triangle$,$\triangle = 10$,所以$\square=2\times10 = 20$。
4. 最后,计算$\triangle+\bigcirc+\square$的值:
$\triangle+\bigcirc+\square=10 + 15+20=45$。
【答案】:$45$
1. 首先,根据已知条件进行等量代换:
已知$\triangle+\triangle+\triangle = \bigcirc+\bigcirc$,那么$4$个$\bigcirc$就等于$6$个$\triangle$(因为$4\bigcirc = 2\times(2\bigcirc)$,而$2\bigcirc = 3\triangle$,所以$4\bigcirc=6\triangle$)。
又因为$\bigcirc+\bigcirc+\bigcirc+\bigcirc=\square+\square+\square$,所以$\square+\square+\square = 6\triangle$,则$\square = 2\triangle$。
再由$\triangle+\triangle+\triangle=\bigcirc+\bigcirc$可得$\bigcirc=\frac{3}{2}\triangle$。
2. 然后,将$\bigcirc=\frac{3}{2}\triangle$和$\square = 2\triangle$代入$\triangle+\bigcirc+\bigcirc+\square = 60$中:
得到$\triangle+\frac{3}{2}\triangle+\frac{3}{2}\triangle + 2\triangle=60$。
对等式左边进行合并同类项:$(1 + \frac{3}{2}+\frac{3}{2}+2)\triangle=(1 + 3+2)\triangle=6\triangle$。
即$6\triangle = 60$,解得$\triangle = 10$。
3. 接着,求出$\bigcirc$和$\square$的值:
因为$\bigcirc=\frac{3}{2}\triangle$,$\triangle = 10$,所以$\bigcirc=\frac{3}{2}\times10 = 15$。
因为$\square = 2\triangle$,$\triangle = 10$,所以$\square=2\times10 = 20$。
4. 最后,计算$\triangle+\bigcirc+\square$的值:
$\triangle+\bigcirc+\square=10 + 15+20=45$。
【答案】:$45$
查看更多完整答案,请扫码查看


