四、下面是从不同位置观察同一个物体所看到的图形。哪个物体符合要求?在括号里画“√”。
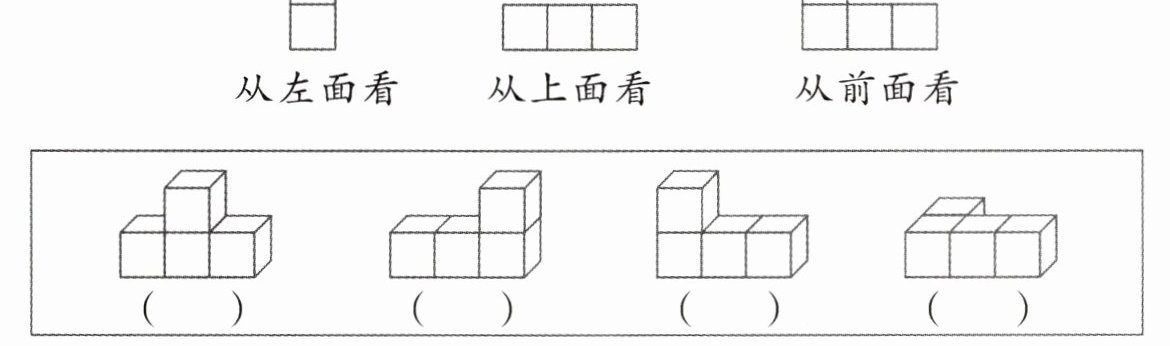
( )( )(

( )( )(
√
)( )
答案:
( )( )(√)( )
动脑筋排一排
下图是一个正方形的城楼,每个角上和每条边的中间都有一个哨位,每个哨位最多可站 2 名哨兵。请你分别按下面的要求排一排(可将哨兵数填入表示哨位的方框中)。
1. 若每个哨位上站 1 名哨兵,城楼的每一边看上去都有几名哨兵?
2. 有 12 名哨兵,如何安排,使得城楼的每一边看上去都有 4 名哨兵?四个角的哨位各站 2 名哨兵(答案不唯一)
3. 要使城楼的每一边看上去都有 5 名哨兵,哨兵的总数也只有 12 名,应如何安排?四个角的哨位各站 2 名哨兵,每条边中间的哨位各站 1 名哨兵(答案不唯一)
下图是一个正方形的城楼,每个角上和每条边的中间都有一个哨位,每个哨位最多可站 2 名哨兵。请你分别按下面的要求排一排(可将哨兵数填入表示哨位的方框中)。
1. 若每个哨位上站 1 名哨兵,城楼的每一边看上去都有几名哨兵?
3
2. 有 12 名哨兵,如何安排,使得城楼的每一边看上去都有 4 名哨兵?四个角的哨位各站 2 名哨兵(答案不唯一)
3. 要使城楼的每一边看上去都有 5 名哨兵,哨兵的总数也只有 12 名,应如何安排?四个角的哨位各站 2 名哨兵,每条边中间的哨位各站 1 名哨兵(答案不唯一)
答案:
【解析】:
1. 正方形有四条边,每条边有$3$个哨位(角上的哨位会被相邻两边共用),每个哨位$1$名哨兵,每边看上去有$3$名哨兵。
2. 每边要看上去有$4$名哨兵,四条边若不考虑重复计算有$4×4 = 16$名,实际$12$名,多算了$16 - 12 = 4$名,因为四个角的哨位多算了一次,所以四个角每个角站$2$名,每条边中间站$0$名(答案不唯一,只要保证四个角各$2$名,中间哨位人数安排合理即可)。
3. 每边要看上去有$5$名哨兵,四条边若不考虑重复计算有$5×4 = 20$名,实际$12$名,多算了$20 - 12 = 8$名,因为四个角的哨位多算了一次,所以四个角每个角站$2$名,每条边中间站$1$名(答案不唯一,只要保证四个角各$2$名,中间哨位人数安排合理即可)。
【答案】:
1. $3$
2. 四个角的哨位各站$2$名哨兵(答案不唯一)
3. 四个角的哨位各站$2$名哨兵,每条边中间的哨位各站$1$名哨兵(答案不唯一)
1. 正方形有四条边,每条边有$3$个哨位(角上的哨位会被相邻两边共用),每个哨位$1$名哨兵,每边看上去有$3$名哨兵。
2. 每边要看上去有$4$名哨兵,四条边若不考虑重复计算有$4×4 = 16$名,实际$12$名,多算了$16 - 12 = 4$名,因为四个角的哨位多算了一次,所以四个角每个角站$2$名,每条边中间站$0$名(答案不唯一,只要保证四个角各$2$名,中间哨位人数安排合理即可)。
3. 每边要看上去有$5$名哨兵,四条边若不考虑重复计算有$5×4 = 20$名,实际$12$名,多算了$20 - 12 = 8$名,因为四个角的哨位多算了一次,所以四个角每个角站$2$名,每条边中间站$1$名(答案不唯一,只要保证四个角各$2$名,中间哨位人数安排合理即可)。
【答案】:
1. $3$
2. 四个角的哨位各站$2$名哨兵(答案不唯一)
3. 四个角的哨位各站$2$名哨兵,每条边中间的哨位各站$1$名哨兵(答案不唯一)
查看更多完整答案,请扫码查看


