《2025年暑假作业及活动新疆文化出版社三年级数学》

一、直接写得数。
20×30= 25×40= 80×900= 270÷9=
240÷2= 11.5-2.8= 43×20= 660÷3=
3.5-2.7= 240-90= 22×4= 515÷5=
1-0.7= 3500÷7= 5500÷5= 7200÷9=

答案： 1. $20×30$，先计算$2×3 = 6$，再在积的末尾添上两个$0$，结果是$600$。
2. $25×40$，先算$25×4 = 100$，再在积的末尾添上一个$0$，结果是$1000$。
3. $80×900$，先算$8×9 = 72$，再在积的末尾添上三个$0$，结果是$72000$。
4. $270÷9$，根据乘法口诀“三九二十七”，$27÷9 = 3$，所以$270÷9 = 30$。
5. $240÷2$，$24÷2 = 12$，所以$240÷2 = 120$。
6. $11.5 - 2.8$，小数点对齐，从最低位减起，$5 - 8$不够减，从个位借$1$当$10$，$15 - 8 = 7$，个位$0 - 2$不够减，从十位借$1$当$10$，$10 - 2 = 8$，十位$1$被借走$1$剩$0$，结果是$8.7$。
7. $43×20$，先算$43×2 = 86$，再在积的末尾添上一个$0$，结果是$860$。
8. $660÷3$，$66÷3 = 22$，所以$660÷3 = 220$。
9. $3.5 - 2.7$，小数点对齐，$5 - 7$不够减，从个位借$1$当$10$，$15 - 7 = 8$，个位$3$被借走$1$剩$2$，$2 - 2 = 0$，结果是$0.8$。
10. $240 - 90$，$40 - 90$不够减，从百位借$1$当$100$，$140 - 90 = 50$，百位$2$被借走$1$剩$1$，结果是$150$。
11. $22×4$，$20×4 = 80$，$2×4 = 8$，$80 + 8 = 88$。
12. $515÷5$，百位$5÷5 = 1$，十位$1÷5$不够商$1$，商$0$占位，$15÷5 = 3$，结果是$103$。
13. $1 - 0.7$，$1$可以写成$1.0$，$0 - 7$不够减，从个位借$1$当$10$，$10 - 7 = 3$，个位$1$被借走$1$剩$0$，结果是$0.3$。
14. $3500÷7$，$35÷7 = 5$，再在商的末尾添上两个$0$，结果是$500$。
15. $5500÷5$，$55÷5 = 11$，再在商的末尾添上两个$0$，结果是$1100$。
16. $7200÷9$，$72÷9 = 8$，再在商的末尾添上两个$0$，结果是$800$。
$20×30 = 600$；$25×40 = 1000$；$80×900 = 72000$；$270÷9 = 30$；$240÷2 = 120$；$11.5 - 2.8 = 8.7$；$43×20 = 860$；$660÷3 = 220$；$3.5 - 2.7 = 0.8$；$240 - 90 = 150$；$22×4 = 88$；$515÷5 = 103$；$1 - 0.7 = 0.3$；$3500÷7 = 500$；$5500÷5 = 1100$；$7200÷9 = 800$。

二、我会连。

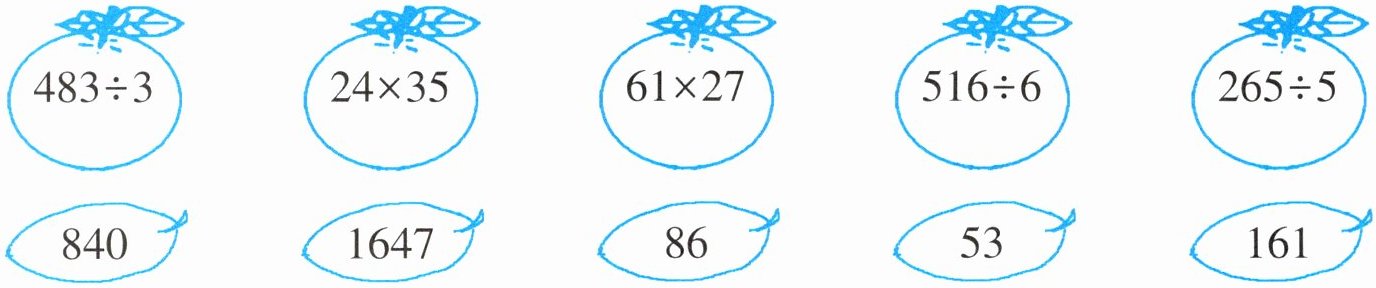
答案： $483\div3 = 161$，计算时，$4\div3 = 1\cdots\cdots1$，$18\div3 = 6$，$3\div3 = 1$，所以商是$161$。
$24\times35$，先算$24\times30 = 720$，再算$24\times5 = 120$，最后$720 + 120 = 840$。
$61\times27$，先算$61\times20 = 1220$，再算$61\times7 = 427$，最后$1220 + 427 = 1647$。
$516\div6$，$5\lt6$，看前两位$51\div6 = 8\cdots\cdots3$，$36\div6 = 6$，所以商是$86$。
$265\div5$，$2\lt5$，看前两位$26\div5 = 5\cdots\cdots1$，$15\div5 = 3$，所以商是$53$。
$483\div3$连$161$；$24\times35$连$840$；$61\times27$连$1647$；$516\div6$连$86$；$265\div5$连$53$。

1. 饲养场一共养鸡多少只？

答案： $ 38 \times 2 \times 4 = 304 $（只）

2. 每个盒子可以装120颗 ,现在有520颗 ,4个盒子能装下吗？

答案： $ 120 \times 4 = 480 $（颗） $ 480 ＜ 520 $ 不能装下

四、请你计算下面图形的面积和周长。

答案： - 对于左边长方形：
- 面积：根据长方形面积公式$S = a\times b$（其中$a$为长，$b$为宽），这里$a = 6$分米，$b = 5$分米，所以面积$S=6\times5 = 30$平方分米。
- 周长：根据长方形周长公式$C=(a + b)\times2$，则$C=(6 + 5)\times2=11\times2 = 22$分米。
- 对于右边图形：
- 面积：可将其看作两个长方形面积之和。上面长方形面积$S_1=2\times(4 - 2)=2\times2 = 4$平方米，下面长方形面积$S_2=(2 + 2)\times2=4\times2 = 8$平方米，总面积$S = S_1+S_2=4 + 8=12$平方米。
- 周长：通过平移线段，可发现该图形周长等于长为$(2 + 2)$米、宽为$4$米的长方形周长。根据长方形周长公式$C=(a + b)\times2$，这里$a=2 + 2 = 4$米，$b = 4$米，所以$C=(4 + 4)\times2=16$米。
- 左边长方形：面积是$30$平方分米，周长是$22$分米。
- 右边图形：面积是$12$平方米，周长是$16$米。