2025年时习之暑假衔接七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
19.(8分)已知点$P(2-m,-3m+1)$,解答下列各题:
(1)若点P在x轴上,求出点P的坐标;
(2)若点Q的坐标为$(4,-1)$,且$PQ// y$轴,求PQ的长.
(1)若点P在x轴上,求出点P的坐标;
(2)若点Q的坐标为$(4,-1)$,且$PQ// y$轴,求PQ的长.
答案:
解:
(1) 因为点$P$在$x$轴上,纵坐标为$0$,所以$-3m + 1 = 0$,解得$m = \frac{1}{3}$。所以$P(\frac{5}{3},0)$。
(2)$PQ// y$轴,则$P$,$Q$两点横坐标相等,所以$2 - m = 4$,解得$m = -2$。所以$P(4,7)$。所以$PQ = 7 - (-1) = 8$。
(1) 因为点$P$在$x$轴上,纵坐标为$0$,所以$-3m + 1 = 0$,解得$m = \frac{1}{3}$。所以$P(\frac{5}{3},0)$。
(2)$PQ// y$轴,则$P$,$Q$两点横坐标相等,所以$2 - m = 4$,解得$m = -2$。所以$P(4,7)$。所以$PQ = 7 - (-1) = 8$。
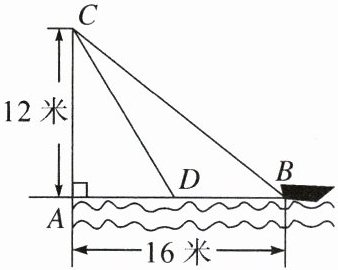
20.(8分)如图,在离水面高度为12米的岸上有人用绳子拉离岸16米的船,若此人以每分钟1米的速度收绳,则5分钟后船向岸边移动的距离BD为多少米?

答案:
解:在$Rt\triangle ABC$中,$AC = 12$米,$AB = 16$米,所以$BC^{2} = AB^{2} + AC^{2} = 16^{2} + 12^{2} = 400$。所以$BC = 20$米。5分钟后,$CD = 20 - 1×5 = 15$(米),所以在$Rt\triangle ACD$中,$AD^{2} = CD^{2} - AC^{2} = 15^{2} - 12^{2} = 81$。所以$AD = 9$米。所以$BD = AB - AD = 16 - 9 = 7$(米)。
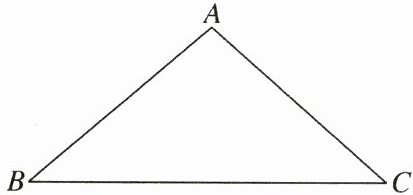
21.(8分)如图,在$\triangle ABC$中,按要求完成尺规作图.
(1)①求作BC边上一点D,使$∠BAD= ∠DAC$;
②求作线段AC的对称轴直线l,交AD于点G;
③连接GC;
(2)在(1)中得到的图形中,若$∠B= 40^{\circ },∠BCA= 2α$,则$∠AGC$的度数为______(用含α的式子表示).
(1)①求作BC边上一点D,使$∠BAD= ∠DAC$;
②求作线段AC的对称轴直线l,交AD于点G;
③连接GC;
(2)在(1)中得到的图形中,若$∠B= 40^{\circ },∠BCA= 2α$,则$∠AGC$的度数为______(用含α的式子表示).

答案:
解:
(1) 如图。
① 点$D$即为所求;
② 直线$l$即为所求;
③ 连接$GC$。

(2)$40^{\circ} + 2\alpha$
解:
(1) 如图。
① 点$D$即为所求;
② 直线$l$即为所求;
③ 连接$GC$。

(2)$40^{\circ} + 2\alpha$
查看更多完整答案,请扫码查看


