2025年成才之路高中新课程学习指导高中化学选择性必修2人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中化学选择性必修2人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
11. Li₂O具有反萤石结构,为立方晶系晶体,其晶胞参数为a pm。该晶胞中离子的分数坐标为:
氧离子:(0, 0, 0);$(\frac{1}{2},\frac{1}{2},0)$;$(\frac{1}{2},0,\frac{1}{2})$;$(0,\frac{1}{2},\frac{1}{2})$;…
锂离子:$(\frac{1}{4},\frac{1}{4},\frac{1}{4})$;$(\frac{1}{4},\frac{3}{4},\frac{1}{4})$;$(\frac{3}{4},\frac{1}{4},\frac{1}{4})$;$(\frac{3}{4},\frac{3}{4},\frac{1}{4})$;…
- (1)在图中画出氧化锂晶胞沿x轴投影的俯视图。
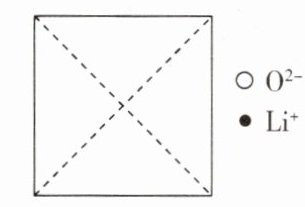
- (2)锂离子的配位数为 。
- (3)设$N_{A}$为阿伏加德罗常数的值,氧化锂晶体的密度为 g·cm⁻³(列出计算表达式)。
氧离子:(0, 0, 0);$(\frac{1}{2},\frac{1}{2},0)$;$(\frac{1}{2},0,\frac{1}{2})$;$(0,\frac{1}{2},\frac{1}{2})$;…
锂离子:$(\frac{1}{4},\frac{1}{4},\frac{1}{4})$;$(\frac{1}{4},\frac{3}{4},\frac{1}{4})$;$(\frac{3}{4},\frac{1}{4},\frac{1}{4})$;$(\frac{3}{4},\frac{3}{4},\frac{1}{4})$;…
- (1)在图中画出氧化锂晶胞沿x轴投影的俯视图。

- (2)锂离子的配位数为 。
- (3)设$N_{A}$为阿伏加德罗常数的值,氧化锂晶体的密度为 g·cm⁻³(列出计算表达式)。
答案:
 @@4@@$\frac{4\times30}{N_{A}\times a^{3}\times10^{-30}}$
@@4@@$\frac{4\times30}{N_{A}\times a^{3}\times10^{-30}}$
 @@4@@$\frac{4\times30}{N_{A}\times a^{3}\times10^{-30}}$
@@4@@$\frac{4\times30}{N_{A}\times a^{3}\times10^{-30}}$ 12. (2023·南宁高二检测)
- (1)Li₂O具有反萤石结构,晶胞如图所示。已知晶胞参数为0.465 nm,阿伏加德罗常数的值为$N_{A}$,则Li₂O的密度为 g·cm⁻³(列出计算式)。
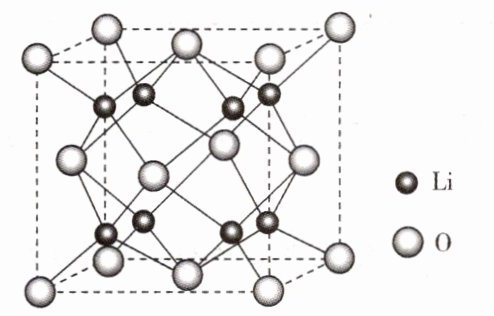
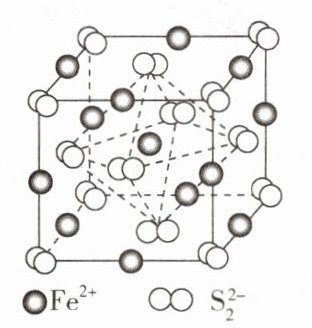
- (2)FeS₂晶体的晶胞如图所示。晶胞棱长为a nm、FeS₂的摩尔质量为M、阿伏加德罗常数的值为$N_{A}$,其晶体密度的计算表达式为 g·cm⁻³;晶胞中Fe²⁺位于$S_{2}^{2 - }$所形成的正八面体的体心,该正八面体的棱长为 nm。
- (1)Li₂O具有反萤石结构,晶胞如图所示。已知晶胞参数为0.465 nm,阿伏加德罗常数的值为$N_{A}$,则Li₂O的密度为 g·cm⁻³(列出计算式)。

- (2)FeS₂晶体的晶胞如图所示。晶胞棱长为a nm、FeS₂的摩尔质量为M、阿伏加德罗常数的值为$N_{A}$,其晶体密度的计算表达式为 g·cm⁻³;晶胞中Fe²⁺位于$S_{2}^{2 - }$所形成的正八面体的体心,该正八面体的棱长为 nm。

答案:
$\frac{8\times7 + 4\times16}{N_{A}(0.4665\times10^{-7})^{3}}$@@$\frac{4M}{N_{A}a^{3}}\times10^{21}$@@$\frac{\sqrt{2}}{2}a$@@解析:
(1)1个氧化锂晶胞含O的个数为$8\times\frac{1}{8}+6\times\frac{1}{2}=4$,含Li的个数为8,$1 cm = 10^{7}nm$,代入密度公式计算可得$Li_{2}O$的密度为$\frac{8\times7 + 4\times16}{N_{A}(0.4665\times10^{-7})^{3}}g\cdot cm^{-3}$。
(2)该晶胞中$Fe^{2 + }$位于棱上和体心,个数为$12\times\frac{1}{4}+1 = 4$,$S^{2 - }$位于顶点和面心,个数为$8\times\frac{1}{8}+6\times\frac{1}{2}=4$,故晶体密度$\rho=\frac{m}{V}=\frac{\frac{4M}{N_{A}}}{(a\times10^{-7})^{3}N_{A}}=\frac{4M}{N_{A}a^{3}}\times10^{21}g\cdot cm^{-3}$;根据晶胞结构,$S^{2 - }$所形成的正八面体的棱长为该晶胞中相邻面的面心之间的连线之长,即为晶胞棱长的$\frac{\sqrt{2}}{2}$,故该正八面体的棱长为$\frac{\sqrt{2}}{2}a$ nm。
(1)1个氧化锂晶胞含O的个数为$8\times\frac{1}{8}+6\times\frac{1}{2}=4$,含Li的个数为8,$1 cm = 10^{7}nm$,代入密度公式计算可得$Li_{2}O$的密度为$\frac{8\times7 + 4\times16}{N_{A}(0.4665\times10^{-7})^{3}}g\cdot cm^{-3}$。
(2)该晶胞中$Fe^{2 + }$位于棱上和体心,个数为$12\times\frac{1}{4}+1 = 4$,$S^{2 - }$位于顶点和面心,个数为$8\times\frac{1}{8}+6\times\frac{1}{2}=4$,故晶体密度$\rho=\frac{m}{V}=\frac{\frac{4M}{N_{A}}}{(a\times10^{-7})^{3}N_{A}}=\frac{4M}{N_{A}a^{3}}\times10^{21}g\cdot cm^{-3}$;根据晶胞结构,$S^{2 - }$所形成的正八面体的棱长为该晶胞中相邻面的面心之间的连线之长,即为晶胞棱长的$\frac{\sqrt{2}}{2}$,故该正八面体的棱长为$\frac{\sqrt{2}}{2}a$ nm。
13. 分析下列晶体结构。
- (1)已知Cu₂O的立方晶胞结构如图所示。
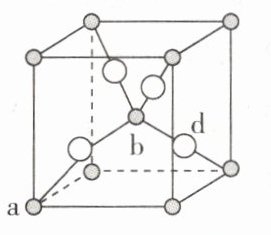
若铜、氧的原子半径分别为$r_{Cu}$ pm、$r_{O}$ pm,Cu₂O晶体的密度为$\rho$ g·cm⁻³,$N_{A}$是阿伏加德罗常数的值,则该晶胞中原子空间占有率为 ×100%。
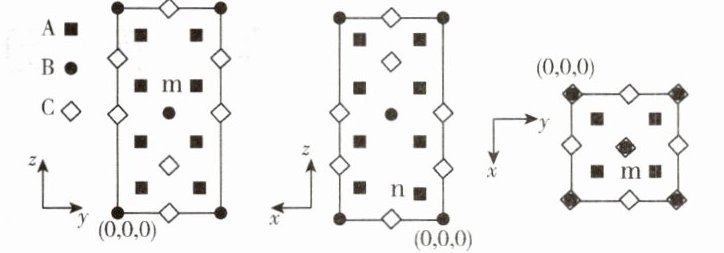
- (2)一种Ag₂HgI₄固体导电材料为四方晶系,其晶胞参数为a pm、a pm和2a pm,晶胞沿x、y、z的方向投影(如图所示),A、B、C表示三种不同原子的投影,标记为n的原子分数坐标为$(\frac{1}{4},\frac{1}{4},\frac{1}{8})$,则m的原子分数坐标为 ,距离Hg最近的Ag有 个。设$N_{A}$为阿伏加德罗常数的值,Ag₂HgI₄的摩尔质量为M g·mol⁻¹,该晶体的密度为 g·cm⁻³(用代数式表示)。
- (3)金属硼氢化物可用作储氢材料。如图是一种金属硼氢化物氨合物的晶体结构示意图。图中八面体的中心代表金属M原子,顶点代表氨分子;四面体的中心代表硼原子,顶点代表氢原子。该晶体属立方晶系,晶胞棱边夹角均为90°,棱长为a pm,密度为$\rho$ g·cm⁻³,阿伏加德罗常数的值为$N_{A}$。

- ①该晶体的化学式为 。
- ②金属M原子与硼原子间最短距离为 pm。
- ③金属M的相对原子质量为 (列出表达式)。
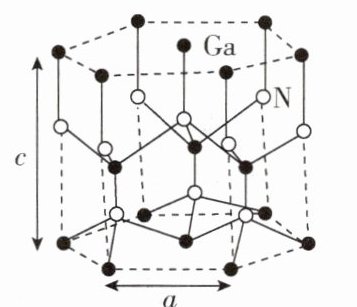
- (4)GaN的一种六方晶胞如图所示,晶胞参数为a nm、c nm。晶体中N原子的配位数为 ;晶体密度$\rho$ = g·cm⁻³(设阿伏加德罗常数的值为$N_{A}$,用a、c、$N_{A}$的代数式表示)。
- (5)一种金属间化合物的晶胞结构如图所示:
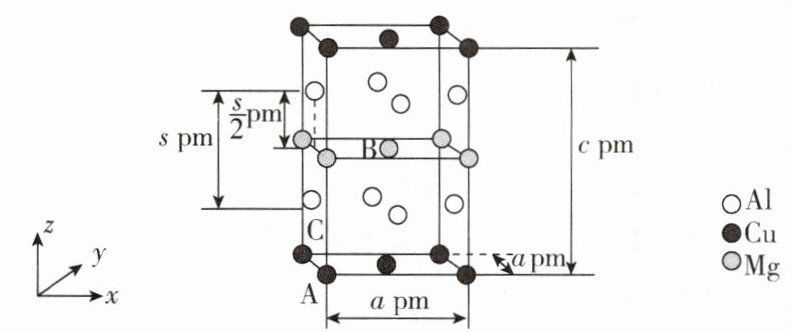
以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称为原子的分数坐标,如A点原子的分数坐标为(0,0,0),B点原子的分数坐标为$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,则C点原子在z轴方向上的分数坐标z = (用含c、s的代数式表示);设Mg、Cu和Al原子半径分别为$r_{Mg}$ pm、$r_{Cu}$ pm、$r_{Al}$ pm,则金属原子的空间占有率为 (列出计算表达式)。
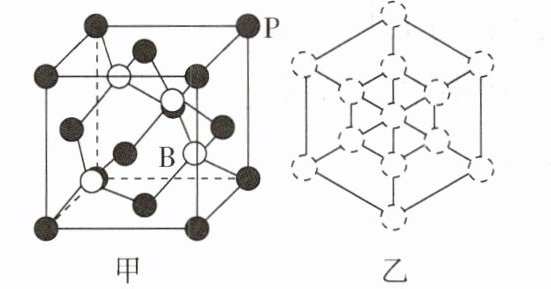
- (6)磷化硼晶胞的示意图如图甲所示,其中实心球表示P原子,空心球表示B原子,晶胞中P原子空间堆积方式为 ;设阿伏加德罗常数的值为$N_{A}$,晶胞参数为a cm,磷化硼晶体的密度为 g·cm⁻³(列出计算式);若磷化硼晶胞沿着体对角线方向的投影如图乙所示(虚线圆圈表示P原子的投影),请在图乙中用实心圆点画出B原子的投影位置 。
- (1)已知Cu₂O的立方晶胞结构如图所示。

若铜、氧的原子半径分别为$r_{Cu}$ pm、$r_{O}$ pm,Cu₂O晶体的密度为$\rho$ g·cm⁻³,$N_{A}$是阿伏加德罗常数的值,则该晶胞中原子空间占有率为 ×100%。
- (2)一种Ag₂HgI₄固体导电材料为四方晶系,其晶胞参数为a pm、a pm和2a pm,晶胞沿x、y、z的方向投影(如图所示),A、B、C表示三种不同原子的投影,标记为n的原子分数坐标为$(\frac{1}{4},\frac{1}{4},\frac{1}{8})$,则m的原子分数坐标为 ,距离Hg最近的Ag有 个。设$N_{A}$为阿伏加德罗常数的值,Ag₂HgI₄的摩尔质量为M g·mol⁻¹,该晶体的密度为 g·cm⁻³(用代数式表示)。

- (3)金属硼氢化物可用作储氢材料。如图是一种金属硼氢化物氨合物的晶体结构示意图。图中八面体的中心代表金属M原子,顶点代表氨分子;四面体的中心代表硼原子,顶点代表氢原子。该晶体属立方晶系,晶胞棱边夹角均为90°,棱长为a pm,密度为$\rho$ g·cm⁻³,阿伏加德罗常数的值为$N_{A}$。

- ①该晶体的化学式为 。
- ②金属M原子与硼原子间最短距离为 pm。
- ③金属M的相对原子质量为 (列出表达式)。
- (4)GaN的一种六方晶胞如图所示,晶胞参数为a nm、c nm。晶体中N原子的配位数为 ;晶体密度$\rho$ = g·cm⁻³(设阿伏加德罗常数的值为$N_{A}$,用a、c、$N_{A}$的代数式表示)。

- (5)一种金属间化合物的晶胞结构如图所示:

以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称为原子的分数坐标,如A点原子的分数坐标为(0,0,0),B点原子的分数坐标为$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,则C点原子在z轴方向上的分数坐标z = (用含c、s的代数式表示);设Mg、Cu和Al原子半径分别为$r_{Mg}$ pm、$r_{Cu}$ pm、$r_{Al}$ pm,则金属原子的空间占有率为 (列出计算表达式)。
- (6)磷化硼晶胞的示意图如图甲所示,其中实心球表示P原子,空心球表示B原子,晶胞中P原子空间堆积方式为 ;设阿伏加德罗常数的值为$N_{A}$,晶胞参数为a cm,磷化硼晶体的密度为 g·cm⁻³(列出计算式);若磷化硼晶胞沿着体对角线方向的投影如图乙所示(虚线圆圈表示P原子的投影),请在图乙中用实心圆点画出B原子的投影位置 。

答案:
$\frac{(4\times\frac{4}{3}\pi r_{Cu}^{3}+2\times\frac{4}{3}\pi r_{O}^{3})\rho N_{A}}{288\times10^{30}}$@@$(\frac{3}{4},\frac{3}{4},\frac{5}{8})$@@8@@$\frac{M}{N_{A}a^{3}}\times10^{30}$@@$M(NH_{3})_{6}B_{2}H_{8}$@@$\frac{\sqrt{3}}{4}a$@@$\frac{\rho a^{3}\times10^{-30}\times N_{A}}{4}-132$@@4@@$\frac{112\sqrt{3}}{N_{A}a^{2}c\times10^{-21}}$@@$\frac{c - s}{2c}$@@$\frac{\frac{4}{3}\pi(2\times r_{Mg}^{3}+2\times r_{Cu}^{3}+4\times r_{Al}^{3})}{a^{2}c}\times100\%$@@面心立方最密堆积@@$\frac{11\times4 + 31\times4}{N_{A}\times a^{3}}$@@
$\frac{(4\times\frac{4}{3}\pi r_{Cu}^{3}+2\times\frac{4}{3}\pi r_{O}^{3})\rho N_{A}}{288\times10^{30}}$@@$(\frac{3}{4},\frac{3}{4},\frac{5}{8})$@@8@@$\frac{M}{N_{A}a^{3}}\times10^{30}$@@$M(NH_{3})_{6}B_{2}H_{8}$@@$\frac{\sqrt{3}}{4}a$@@$\frac{\rho a^{3}\times10^{-30}\times N_{A}}{4}-132$@@4@@$\frac{112\sqrt{3}}{N_{A}a^{2}c\times10^{-21}}$@@$\frac{c - s}{2c}$@@$\frac{\frac{4}{3}\pi(2\times r_{Mg}^{3}+2\times r_{Cu}^{3}+4\times r_{Al}^{3})}{a^{2}c}\times100\%$@@面心立方最密堆积@@$\frac{11\times4 + 31\times4}{N_{A}\times a^{3}}$@@

查看更多完整答案,请扫码查看


