《2025年天利38套常考基础题高中物理》

6.有位网友发布了自己乘坐复兴号动车组在行驶过程中超过旁边和谐号动车组的视频，让大家又一次感受到了中国新速度！和谐号动车与复兴号动车相继从同一站点由静止出发，沿同一方向做匀加速直线运动.两车的速度—时间图像如图所示，下列说法正确的是 （ 　　）
　　　　　　　　　　　　　　　
A.和谐号动车和复兴号动车在加速过程中的加速度分别为0.5 m/s²、1 m/s²
B.复兴号动车追上和谐号动车前，t＝70 s时，两车相距最远
C.复兴号动车追上和谐号动车前，两车最远相距2 450 m
D.t＝140 s时，复兴号动车追上和谐号动车

答案： AC 速度—时间图像、运动学规律 速度—时间图像的斜率表示物体的加速度，故和谐号动车和复兴号动车在加速过程中的加速度分别为$a_{1}=\frac{\Delta v_{1}}{\Delta t_{1}}=\frac{70 - 0}{140 - 0}\ m/s^{2}=0.5\ m/s^{2}$，$a_{2}=\frac{\Delta v_{2}}{\Delta t_{2}}=\frac{70 - 0}{140 - 70}\ m/s^{2}=1\ m/s^{2}$，A正确；和谐号动车与复兴号动车从同一站点由静止出发，$0～140\ s$内，和谐号的速度一直比复兴号的大，两者间距逐渐增大，$140\ s$以后，复兴号的速度一直比和谐号的大，两者间距逐渐减小，故$t = 140\ s$时，两车相距最远，最远距离$x = x_{和}-x_{复}=\frac{70×140}{2}\ m-\frac{70×70}{2}\ m = 2450\ m$，C正确，BD错误.
关键点拨
(1)理解速度—时间图像的物理意义，图线的斜率表示加速度，图线与时间轴围成的面积表示位移.
(2)在追及相遇问题中，速度相等是两物体相距最近或最远的临界条件.

7.在赣州市南河大桥扩建工程中，双向桥梁已完成了某一通车方向的建设，为保持双向车辆正常通行，临时将其改成双向车道.如图所示，引桥与桥面对接处，有两车道合并一车道的对接口，A、B两车相距s₀＝4 m时，B车正以vB＝4 m/s速度匀速行驶，A车正以vA＝7 m/s的速度借道超越同向行驶的B车，此时A车司机发现前方距离车头s＝16 m处的并道对接口.A、B两车长度均为L＝4 m，且不考虑A车变道过程的影响.
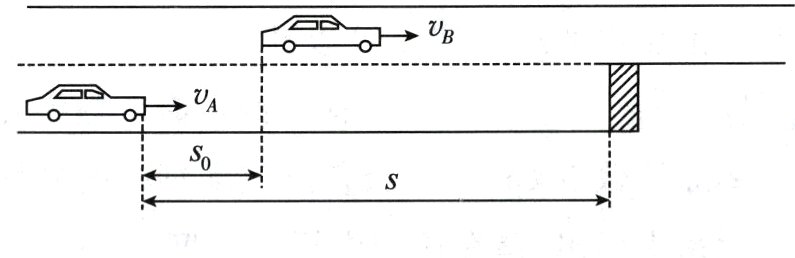
(1)若A车司机放弃超车，而立即驶入与B车相同的行驶车道，A车至少以多大的加速度刹车匀减速，才能避免与B车相撞；
(2)若A车司机加速超车，A车的最大加速度为a＝3 m/s²，请通过计算分析A车能否实现安全超车.
　　　　　　　　　　　　　　　　　　　　　

答案： 追及、相遇问题
解：
(1)由题意，“临界点”为，$A$车与$B$车恰好不相撞，二者速度相同时，由运动学公式有
$v_{B}=v_{A}-a_{0}t_{0}$
$A$车运动的位移$x_{A}=v_{A}t_{0}-\frac{1}{2}a_{0}t_{0}^{2}$
$B$车运动的位移$x_{B}=v_{B}t_{0}$
$s_{0}=x_{A}-x_{B}$
由以上各式可得$a_{0}=1.125\ m/s^{2}$
(2)$A$车如果能超过$B$车则有
$A$车运动的位移$x_{1}=v_{A}t+\frac{1}{2}at^{2}$
$B$车运动的位移$x_{2}=v_{B}t$
$s_{0}+2L=x_{1}-x_{2}$
由以上各式可得$A$车的位移$x_{1}=20\ m$
因$x_{1}＞s$，则$A$车不能实现安全超车