《2025年天利38套常考基础题高中物理》

7.某次演习中，救援飞机水平匀速飞行，朝前方落水者释放救生设备，该设备越过了落水者.再次释放时，设释放点与落水者间的水平距离不变，忽略空气阻力，为了使救生设备准确落到落水者处，则飞机可采取的措施有(　　　)
A.高度不变，适当降低飞行速度 B.高度不变，适当增加飞行速度 C.速度不变，适当降低飞行高度 D.速度不变，适当增加飞行高度

答案： AC 平抛运动规律 由平抛运动规律得$x = v_{0}t$，$h=\frac{1}{2}gt^{2}$，联立解得$x = v_{0}\sqrt{\frac{2h}{g}}$，若飞行高度不变，适当降低飞行速度，则水平位移减小，救生设备可准确落到落水者处，A 正确，B 错误；若飞行速度不变，适当降低飞行高度，则水平位移减小，救生设备可准确落到落水者处，C 正确，D 错误。

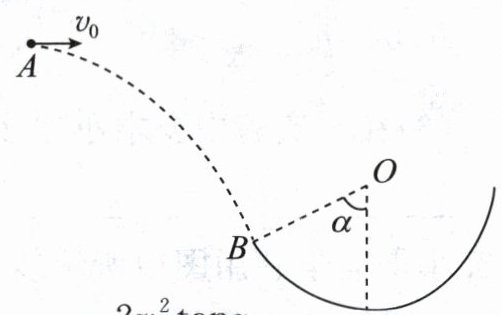
8.如图所示，B为竖直圆轨道的左端点，它和圆心O的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A点以速度v0水平抛出，恰好沿B点的切线方向进入圆轨道.已知重力加速度为g，不计空气阻力，则下列说法中正确的是(　　　)

答案：
CD 平抛运动规律等知识 将小球在 B 点的速度分解，如图所示 ，由几何知识得，$v_{y}=v_{0}\tan\alpha$，由$v_{y}=gt$得，小球从 A 运动到 B 的时间$t=\frac{v_{0}\tan\alpha}{g}$，A 错误；A、B 之间的水平距离$x_{AB}=v_{0}t=\frac{v_{0}^{2}\tan\alpha}{g}$，B 错误；A、B 之间的竖直高度$h=\frac{1}{2}v_{y}t=\frac{v_{0}^{2}\tan^{2}\alpha}{2g}$，C 正确；运动到 B 点的速度大小$v=\frac{v_{0}}{\cos\alpha}$，D 正确。

9.(2022·山东卷)如图所示，某同学将离地1.25 m的网球以13 m/s的速度斜向上击出，击球点到竖直墙壁的距离4.8 m，当网球竖直分速度为零时，击中墙壁上离地高度为8.45 m的P点，网球与墙壁碰撞后，垂直墙面速度分量大小变为碰前的0.75，平行墙面的速度分量不变，重力加速度g取10 m/s²，网球碰墙后的速度大小v和着地点到墙壁的距离d分别为(　　　)

答案： BD 平抛运动 设网球抛出时水平方向平行于墙方向的速度为$v_{x}$，水平方向垂直于墙方向的速度为$v_{y}$，竖直方向的速度为$v_{z}$，所以有$v_{0}^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}$，由竖直方向运动有$v_{z}^{2}=2gh$，所以竖直方向的速度$v_{z}=12\ m/s$，网球碰撞前在空中的运动时间$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2(8.45 - 1.25)}{10}}\ s=1.2\ s$，垂直于墙方向的速度$v_{y}=\frac{d}{t}=\frac{4.8}{1.2}\ m/s = 4\ m/s$，所以网球抛出时平行于墙方向的速度$v_{x}=3\ m/s$，与墙碰撞后网球垂直于墙方向的速度$v_{y}'=0.75v_{y}=3\ m/s$，所以网球碰墙后的速度大小$v=\sqrt{v_{x}^{2}+v_{y}'^{2}}=3\sqrt{2}\ m/s$，故 A 错误，B 正确；网球碰墙后到落地的时间$t'=\sqrt{\frac{2h'}{g}}=\sqrt{\frac{2\times8.45}{10}}\ s=1.3\ s$，小球落地时与墙的距离$d = v_{y}'t'=3.9\ m$，故 C 错误，D 正确。
易错警示：这是一个立体情境的题目，首先学生要建立立体情境，然后要注意小球碰墙前上升的最大高度和碰墙后下落的高度不同，所以这两个过程的时间也不同。

10.游戏中有一个小球A自由下落，从等高处水平抛出一个相同小球B，不计空气阻力，则(　　　)

A.小球B一定能击中小球A

B.若要击中小球A，则必须在A下落同时抛出小球B

C.小球A下落后再将小球B抛出，仍可能击中小球A

D.若小球B斜向上抛出，同时释放小球A，则一定无法击中

答案： BD 抛体运动 小球 A 自由下落，小球 B 从等高处水平抛出，小球 B 在竖直方向做自由落体运动，要想击中小球 A，两个小球下落的高度必须相等，所以必须同时抛出，小球 B 才能击中小球 A，B 项正确，AC 项错误；小球 B 斜向上抛出，小球 B 在竖直方向上做竖直上抛运动，同时出发的小球 A 做自由落体运动，两者竖直位移一定不同，故一定无法击中，D 项正确。
方法提炼：A、B 两小球分别做自由落体运动和平抛运动，若小球 B 要击中小球 A，则要求两者同一时刻到达同一竖直高度。