《2025年全优课堂考点集训与满分备考九年级数学下册人教版》

9.下列各组图形中一定是相似形的是　(　　　)
A.两个直角三角形
　B.两个等边三角形
C.两个菱形　　　　
　D.两个矩形

答案： B

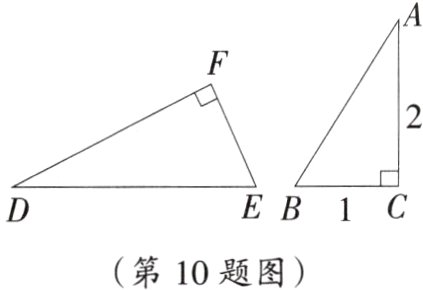
10.如图,Rt△ABC与Rt△DEF相似,相似比为$\frac{2}{3}$,若AC=2,BC=1,则DE=　　　　　(　　　)

A.$2\sqrt{5}$　　　　　
　B.$3\sqrt{5}$
C.$\frac{3\sqrt{5}}{2}$　　　　　
　D.$\frac{2\sqrt{5}}{3}$

答案： C 提示：由Rt△$ABC$与Rt△$DEF$相似，得$\frac{AB}{DE}$ = $\frac{2}{3}$，由勾股定理得$AB$ = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$，从而得到$\frac{\sqrt{5}}{DE}$ = $\frac{2}{3}$，
∴$DE$ = $\frac{3\sqrt{5}}{2}$.

11.如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗？答:__________

答案： 不相似 提示：
∵木质边框宽7.5 cm = 0.075 m，
∴木质边框外边缘所形成的矩形的长为3 + 2×0.075 = 3.15(m)，木质边框外边缘所形成的矩形的宽为1.5 + 2×0.075 = 1.65(m)，
∴边框的内外边缘的长度之比为$\frac{3}{3.15}$ = $\frac{20}{21}$，边框的内外边缘的宽度之比为$\frac{1.5}{1.65}$ = $\frac{10}{11}$，
∵$\frac{20}{21}$≠$\frac{10}{11}$，
∴边框的内外边缘所成的矩形不相似.

12.如图,四边形ABCD与四边形GFEH相似且∠A=∠G=70°,∠B=60°,∠E=120°,DC=24,HE=18,HG=21,则∠D=______,∠F=______,AD=______.

答案： 110° 60° 28
提示：
∵四边形$ABCD$与四边形$GFEH$相似，
∴∠$C$ = ∠$E$ = 120°，∠$F$ = ∠$B$ = 60°，
∵∠$A$ = ∠$G$ = 70°，∠$B$ = 60°，∠$C$ = 120°，
∴∠$D$ = 360° - ∠$A$ - ∠$B$ - ∠$C$ = 360° - 70° - 60° - 120° = 110°；
∵四边形$ABCD$与四边形$GFEH$相似，
∴$\frac{DC}{HE}$ = $\frac{AD}{HG}$，
∵$DC$ = 24，$HE$ = 18，$HG$ = 21，
∴$\frac{24}{18}$ = $\frac{AD}{21}$，解得$AD$ = 28.
∴∠$D$ = 110°，∠$F$ = 60°，$AD$ = 28.

13.如图,在▱ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点，这样形成一个▱FEMN,你能证明▱ABCD与▱FEMN相似吗？

答案： 证明：
∵点$F$，$E$，$M$，$N$分别是$AO$，$BO$，$CO$，$DO$的中点，
∴$FN$//$EM$//$AD$//$BC$，$EF$//$NM$//$AB$//$CD$，
∴$EM$ = $FN$ = $\frac{1}{2}CB$，$EF$ = $NM$ = $\frac{1}{2}AB$，
∠$OEM$ = ∠$OBC$，∠$OEF$ = ∠$OBA$，
∴$\frac{EM}{BC}$ = $\frac{MN}{CD}$ = $\frac{FN}{AD}$ = $\frac{EF}{AB}$，∠$FEM$ = ∠$ABC$，
同理可证∠$FEM$ = ∠$FNM$ = ∠$ABC$ = ∠$ADC$，∠$BAD$ = ∠$EFN$ = ∠$BCD$ = ∠$EMN$，
∴□$ABCD$与□$FEMN$相似.

14.已知三条线段的长分别为1cm,2cm, $\sqrt{2}$cm,如果另外一条线段与它们是成比例线段,那么另外一条线段的长为__________________.

答案： 2$\sqrt{2}$ cm或$\frac{\sqrt{2}}{2}$ cm或$\sqrt{2}$ cm
提示：设另外一条线段的长为$a$，由题意，得$\frac{1}{2}$ = $\frac{\sqrt{2}}{a}$或$\frac{1}{a}$ = $\frac{2}{\sqrt{2}}$或$\frac{a}{1}$ = $\frac{2}{\sqrt{2}}$，解得$a$ = 2$\sqrt{2}$ cm或$\frac{\sqrt{2}}{2}$ cm或$\sqrt{2}$ cm.

15.如图所示的三个矩形中,其中相似形是　　　　　　　　　　　　　　　　(　　　)

A.甲与乙　　　　　
　B.乙与丙
C.甲与丙　　　　　
　D.以上都不对

答案： B 提示：因为$\frac{4}{3}$≠$\frac{2}{1}$，故甲与乙不相似；因为$\frac{2}{1}$ = $\frac{4}{2}$，故乙与丙相似；因为$\frac{4}{3}$≠$\frac{4}{2}$，故甲与丙不相似.

16.下列各组线段中,成比例线段的是　(　　　)
A.4cm,6cm,5cm,8cm
B.2cm,5cm,6cm,8cm
C.3cm,6cm,9cm,18cm
D.1cm,2cm,3cm,4cm

答案： C 提示：只有C项中$\frac{3}{6}$ = $\frac{9}{18}$.

17.几何直观如图,▱ABCD与▱A'B'C'D'的形状相同,则A'D'的长度为　　　　　　(　　　)

A.2cm　　　　　　
　B.$\frac{2}{3}$cm
C.$\frac{4}{3}$cm　　　　　
　D.$\frac{3}{2}$cm

答案： C 提示：利用相似多边形的对应边成比例计算.$\frac{A'B'}{AB}$ = $\frac{A'D'}{AD}$，即$\frac{2}{3}$ = $\frac{A'D'}{2}$，
∴$A'D'$ = $\frac{4}{3}$ cm.

18.一个五边形的边长分别为2,3,4,5,6,另一个五边形和这个五边形相似,且最短边长为6,则最长边长为　　　　　　　　　(　　　)
A.18　
　B.12　　
　C.24　　
　D.30

答案： A 提示：设另一个多边形的最长边长是$x$，则$\frac{2}{6}$ = $\frac{6}{x}$，解得$x$ = 18.

19.易错题下列图形中一定相似的一组是(　　　)
A.邻边对应成比例的两个平行四边形
B.有一条边相等的两个矩形
C.有一个内角相等的两个平行四边形
D.底角都是60°的两个等腰三角形

答案： D 提示：A.邻边对应成比例的两个平行四边形，对应的角不一定相等，因而不一定相似，故错误；
B.有一条边相等的两个矩形，对应边的比不一定相等，因而不一定相似，故错误；
C.有一个内角对应相等的两个平行四边形，对应边的比不一定相等，故错误；
D.底角都是60°的等腰三角形一定是等边三角形，因而一定相似，故正确.