《2025年全优课堂考点集训与满分备考九年级数学下册人教版》

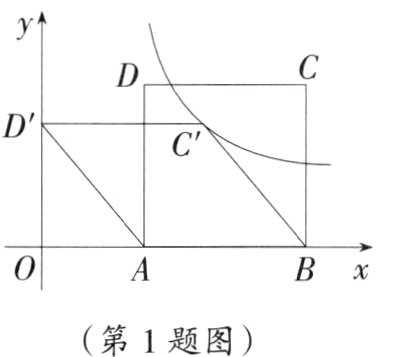
1. 如图，在正方形ABCD中，点C(8,5)，AB边不动，将正方形向左下方推动变形，使点D落在y轴的点D'处，点C落在点C'处，则经过点C'的反比例函数解析式是（ ）

A. $y=\frac{20}{x}$
B. $y=\frac{16}{x}$
C. $y=\frac{12}{x}$
D. $y=\frac{10}{x}$

答案：
A提示:
∵在正方形ABCD中，点C(8,5)，
∴AB = BC = 5，OB = 8，
∴OA = 8 - 5 = 3，
∴A(3,0)，
∵AD' = 5，
∴OD' = 4，
如图，过点C'作C'M⊥OB于点M，
∵BC' = AD'，C'M = OD'，
∴Rt△AOD'≌Rt△BMC'(HL)，
∴MB = OA = 3，
∴C'(5,4)，
∵点C'在反比例函数y = $\frac{k}{x}$的图象上，
∴k = 5×4 = 20，
∴y = $\frac{20}{x}$。

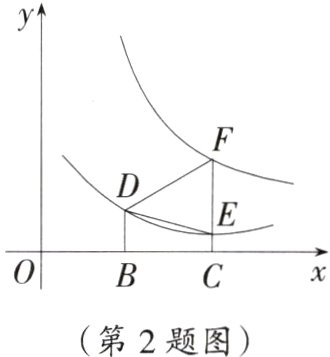
2. 方程思想 如图，△DEF的三个顶点分别在反比例函数$xy = n$与$xy = m(x＞0,m＞n＞0)$的图象上，若$DB\perp x$轴于点B，$FE\perp x$轴于点C，B为OC的中点，△DEF的面积为2，则m，n的关系式是（ ）

A. $m - n = 8$
B. $m + n = 8$
C. $2m - n = 8$
D. $2m + n = 3$

答案： A提示:设D(a,$\frac{n}{a}$)，
则F(2a,$\frac{m}{2a}$)，E(2a,$\frac{n}{2a}$)，
∴$S_{\triangle DEF}=\frac{1}{2}BC\cdot EF=\frac{1}{2}a\times(\frac{m}{2a}-\frac{n}{2a}) = 2$，
整理得m - n = 8。

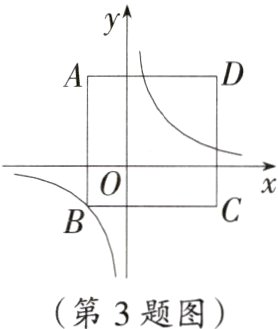
3. 易错题 如图，在平面直角坐标系中，矩形ABCD四个顶点的坐标分别为A(-1,2)，B(-1,-1)，C(3,-1)，D(3,2)，当双曲线$y=\frac{k}{x}(k＞0)$与矩形有四个交点时，k的取值范围是________________.

答案： 0＜k＜1提示:根据反比例函数的对称性，双曲线y = $\frac{k}{x}$(k＞0)与矩形有四个交点，只要反比例函数在第三象限的图象与矩形有2个交点即可，当反比例函数的图象过点B(-1,-1)时，此时k = 1，反比例函数图象与矩形有三个交点，当反比例函数图象与AB有交点时，则当x = -1时，y = -k＞-1，即k＜1；当反比例函数图象与BC有交点时，则当y = -1时，x = -k＞-1，即k＜1；又
∵k＞0，
∴0＜k＜1。

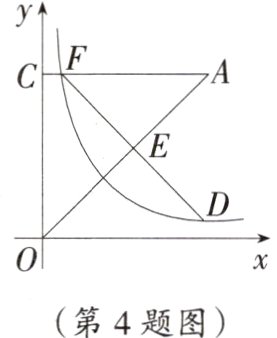
4. 如图，等腰直角三角形AOC中，点C在y轴的正半轴上，$OC = AC = 4$，AC交反比例函数$y=\frac{2}{x}$的图象于点F，过点F作$FD\perp OA$，交OA于点E，交反比例函数图象于另一点D，则点D的坐标为________.

答案： (4,$\frac{1}{2}$)提示:
∵OC = AC = 4，AC交反比例函数y = $\frac{2}{x}$的图象于点F，
∴F的纵坐标为4，代入y = $\frac{2}{x}$求得x = $\frac{1}{2}$，
∴F($\frac{1}{2}$,4)，
∵等腰直角三角形AOC中，∠AOC = 45°，
∴直线OA的解析式为y = x，
∴F关于直线OA的对称点是点D，
∴点D的坐标为(4,$\frac{1}{2}$)。

5. 如图，△$P_1OA_1$，△$P_2A_1A_2$都是等边三角形，点$P_1$，$P_2$在函数$y=\frac{4\sqrt{3}}{x}(x＞0)$的图象上，点$A_1$，$A_2$在x轴上，则线段$P_2A_2$的长度是________.

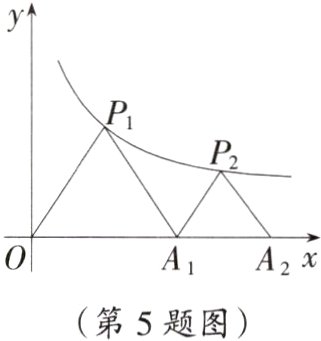
答案：
-4 + 4$\sqrt{2}$提示:如图，作P₁A⊥x轴于A，P₁B⊥y轴于B，P₂D⊥x轴于D，P₂C⊥y轴于C，
∵△P₁OA₁，△P₂A₁A₂是等边三角形，
∴AP₁ = $\sqrt{3}$OA，DP₂ = $\sqrt{3}$A₁D，则OA·AP₁ = 4$\sqrt{3}$，
∴OA = 2，
∴OA₁ = 4，设A₁D = a，则有(4 + a)·$\sqrt{3}$a = 4$\sqrt{3}$，解得a = -2 + 2$\sqrt{2}$或a = -2 - 2$\sqrt{2}$（舍去），则A₁A₂ = 2a = -4 + 4$\sqrt{2}$，
∴P₂A₂ = A₁A₂ = -4 + 4$\sqrt{2}$。

6. 较难题 如图，点A，B分别在x轴和y轴的正半轴上，以线段AB为边在第一象限作等边三角形ABC，$S_{\triangle ABC}=\sqrt{3}$，且$CA// y$轴.
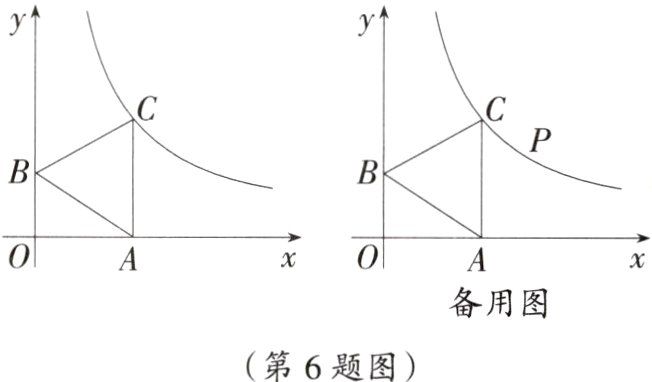
(1)若点C在反比例函数$y=\frac{k}{x}(k\neq0)$的图象上，求该反比例函数的解析式；
(2)在(1)中的反比例函数图象上是否存在点N，使四边形ABCN是菱形，若存在请求出点N的坐标，若不存在，请说明理由；
(3)点P在第一象限的反比例函数图象上，当四边形OAPB的面积最小时，求出点P坐标.

答案：
解:
(1)如图1，作CD⊥y轴于D.
∵CA//y轴，CD⊥y轴，
∴CD//OA，AC//OD，
∴四边形OACD是平行四边形，
∵∠AOD = 90°，
∴四边形OACD是矩形，
∴k = $S_{矩形OACD}=2S_{\triangle ABC}=2\sqrt{3}$，
∴反比例函数的解析式为y = $\frac{2\sqrt{3}}{x}$；

(2)如图2，作BE⊥AC于E，交反比例函数图象于N，连接CN，AN.
∵△ABC是等边三角形，面积为$\sqrt{3}$，
设CE = AE = m，则BE = $\sqrt{3}$m，
∴$\frac{1}{2}\times2m\times\sqrt{3}m=\sqrt{3}$，
∴m = 1或 - 1(舍去)，
∴B(0,1)，C($\sqrt{3}$,2)，A($\sqrt{3}$,0)，
∴N(2$\sqrt{3}$,1)，
∴BE = EN，
∵AC⊥BN，
∴CB = CN，AB = AN，
∵AB = BC，
∴AB = BC = CN = AN，
∴四边形ABCN是菱形，
∴N(2$\sqrt{3}$,1)；

(3)如图3，连接PB，PA，OP.
设P(a,$\frac{2\sqrt{3}}{a}$)。$S_{四边形OAPB}=S_{\triangle POB}+S_{\triangle POA}=\frac{1}{2}\times1\times a+\frac{1}{2}\times\sqrt{3}\times\frac{2\sqrt{3}}{a}=\frac{1}{2}a+\frac{3}{a}=(\sqrt{\frac{1}{2}a}-\sqrt{\frac{3}{a}})^2+\sqrt{6}$，
∴当$\frac{1}{2}a=\frac{3}{a}$时，四边形OAPB的面积最小，解得a = $\sqrt{6}$或 - $\sqrt{6}$（舍去），此时P($\sqrt{6}$,$\sqrt{2}$)。