1. 小明在半径为 5 的圆中测量弦 AB 的长度,下列测量结果中一定错误的是( )
A. 4
B. 5
C. 10
D. 11
A. 4
B. 5
C. 10
D. 11
答案:
2. 如图,已知在⊙O 中,BC 是直径,AB = DC,则下列结论不一定成立的是( )

A. OA = OB = AB
B. ∠AOB = ∠COD
C. $\overset{\frown}{AB}=\overset{\frown}{DC}$
D. O 到 AB,CD 的距离相等

A. OA = OB = AB
B. ∠AOB = ∠COD
C. $\overset{\frown}{AB}=\overset{\frown}{DC}$
D. O 到 AB,CD 的距离相等
答案:
3. 如图,圆上有 A,B,C,D 四个点,AC,BD 交于点 P,则图中与∠C 相等的角是( )

A. ∠A
B. ∠B
C. ∠D
D. ∠APD

A. ∠A
B. ∠B
C. ∠D
D. ∠APD
答案:
4. 下列说法中,正确的是( )
A. 过圆心的直线是圆的直径
B. 直径是圆中最长的弦
C. 相等长度的两条弧是等弧
D. 顶点在圆上的角是圆周角
A. 过圆心的直线是圆的直径
B. 直径是圆中最长的弦
C. 相等长度的两条弧是等弧
D. 顶点在圆上的角是圆周角
答案:
5. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧. 如图①,点 M 表示筒车的一个盛水桶. 如图②,当筒车工作时,盛水桶的运行路径是以轴心 O(O 在水面上方)为圆心的圆,且圆 O 被水面截得的弦 AB 长为 8 米. 若筒车工作时,盛水桶在水面以下的最大深度为 2 米,则这个圆的半径为( )
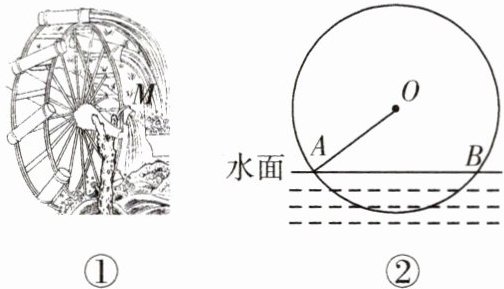
A. 2 米
B. 3 米
C. 4 米
D. 5 米

A. 2 米
B. 3 米
C. 4 米
D. 5 米
答案:
6. 如图,在⊙O 中,OA⊥BC,∠CDA = 22.5°,则∠AOB 的度数为( )

A. 22.5°
B. 30°
C. 45°
D. 60°

A. 22.5°
B. 30°
C. 45°
D. 60°
答案:
7. 如图,已知锐角∠AOB,按如下步骤作图:
①在射线 OA 上取一点 C,以点 O 为圆心,OC 长为半径作 $\overset{\frown}{PQ}$,交射线 OB 于点 D,连接 CD;②分别以点 C,D 为圆心,CD 长为半径作弧,交 $\overset{\frown}{PQ}$ 于点 M,N;③连接 OM,MN,ND. 根据以上作图过程及所作图形,下列结论中错误的是( )
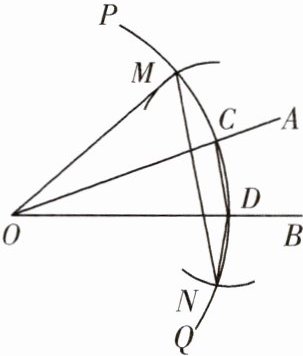
A. ∠COM = ∠COD
B. 若 OM = MN,则∠AOB = 30°
C. MN//CD
D. ∠MOD = 2∠MND
①在射线 OA 上取一点 C,以点 O 为圆心,OC 长为半径作 $\overset{\frown}{PQ}$,交射线 OB 于点 D,连接 CD;②分别以点 C,D 为圆心,CD 长为半径作弧,交 $\overset{\frown}{PQ}$ 于点 M,N;③连接 OM,MN,ND. 根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM = ∠COD
B. 若 OM = MN,则∠AOB = 30°
C. MN//CD
D. ∠MOD = 2∠MND
答案:
8. 学了圆的相关知识后,小亮想到用这种方法测量三角形的角度:将三角形纸片如图放置,使得顶点 C 在量角器的半圆上,纸片另外两边分别与量角器交于 A,B 两点. 点 A,B 对应的度数分别是 72°,14°,这样小亮就能得到∠C 的度数. 请你帮忙算算∠C 的度数是( )

A. 28°
B. 29°
C. 30°
D. 58°

A. 28°
B. 29°
C. 30°
D. 58°
答案:
查看更多完整答案,请扫码查看


