1. 圆周角的概念
顶点在_______,并且两边在圆内的部分分别是圆的_______,像这样的角叫作圆周角.
顶点在_______,并且两边在圆内的部分分别是圆的_______,像这样的角叫作圆周角.
答案:
2. 圆周角定理及推论
定理:圆周角的度数等于它所对弧上的圆心角度数的_______.
推论1:圆周角的度数等于它所对弧的度数的_______.
推论2:同弧或等弧所对的圆周角_______.
定理:圆周角的度数等于它所对弧上的圆心角度数的_______.
推论1:圆周角的度数等于它所对弧的度数的_______.
推论2:同弧或等弧所对的圆周角_______.
答案:
1. 在探究圆周角的度数与它所对弧上圆心角的度数之间的数量关系时,我们分类讨论了如图所示的三种情况,经画图操作并添加辅助线将图②、图③转化为图①,从而证明了$\angle BAC = \frac{1}{2}\angle BOC$,其中体现的数学思想是( )
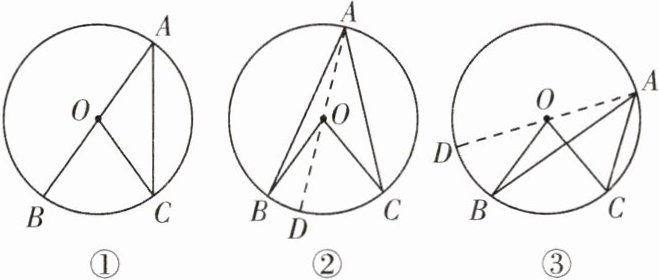
A. 数形结合思想
B. 转化思想
C. 公理化思想
D. 类比思想

A. 数形结合思想
B. 转化思想
C. 公理化思想
D. 类比思想
答案:
2.(柳州中考)如图,在$\odot O$中与$\angle 1$一定相等的角是( )

A. $\angle 2$
B. $\angle 3$
C. $\angle 4$
D. $\angle 5$

A. $\angle 2$
B. $\angle 3$
C. $\angle 4$
D. $\angle 5$
答案:
3. 如图,点$A$,$B$,$C$均在$\odot O$上,若$\angle AOC = 80^{\circ}$,则$\angle ABC$的度数是( )

A. $30^{\circ}$
B. $35^{\circ}$
C. $40^{\circ}$
D. $50^{\circ}$

A. $30^{\circ}$
B. $35^{\circ}$
C. $40^{\circ}$
D. $50^{\circ}$
答案:
4. 如图,点$A$,$B$,$C$在$\odot O$上,$\angle A = 72^{\circ}$,则$\angle OBC$的度数是( )

A. $12^{\circ}$
B. $15^{\circ}$
C. $18^{\circ}$
D. $20^{\circ}$

A. $12^{\circ}$
B. $15^{\circ}$
C. $18^{\circ}$
D. $20^{\circ}$
答案:
5. 如图,以$AB$为直径的半圆上有一点$C$,$\angle C = 25^{\circ}$,则$\overset{\frown}{BC}$的度数为( )

A. $25^{\circ}$
B. $30^{\circ}$
C. $50^{\circ}$
D. $65^{\circ}$

A. $25^{\circ}$
B. $30^{\circ}$
C. $50^{\circ}$
D. $65^{\circ}$
答案:
6. 如图,在$\odot O$中,$A$是$\overset{\frown}{CB}$的中点,$\angle AOB = 40^{\circ}$,则$\angle ADC$的度数是_______.


答案:
7. 如图,将四个边长为1的小正方形拼成一个大正方形,$A$,$B$,$C$,$D$,$O$在小正方形的顶点上,$\odot O$的半径为1,$E$是$\overset{\frown}{CD}$的中点,则$\angle EAB$的度数为_______.
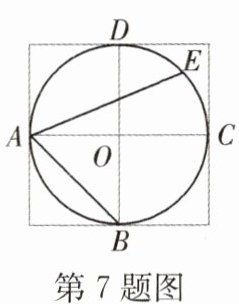

答案:
8.(南京中考)如图,$\odot O$的弦$AB$,$CD$的延长线相交于点$P$,且$AB = CD$. 求证:$PA = PC$.


答案:
查看更多完整答案,请扫码查看


