例1
已知全集I=R,集合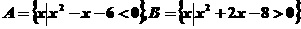 ,
,
 ,
,
(1)试求实数a的取值范围,使 ;
;
(2)试求实数的取值范围,使 .
.
例2
解下列不等式:
注意:这是一组解简单的高次不等式的问题,采用的解法叫做数轴标根法,图中所画的曲线实际上是函数f(x)=(x-x1)(x-x2)…(x-xn)的图象的示意图这一过程中,应当注意两点:(1)最右边的一个区间上,函数图象位于x轴的上方;(2)当相应的方程有偶次重根时,图像与x轴相切.
例3 设a¹b,解关于的不等式:
注意:解含字母系数的不等式,要有对字母作分类讨论的准备,但讨论什么,怎么讨论要在求解过程中看等价变形的要求去定,也可能不必讨论.
例4 解不等式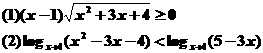
例5 解关于x的不等式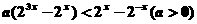
例6 解不等式
注意:化去不等式中的绝对值号转化为不含绝对值号的不等式是此类问题的通常思路,这就要确定log2x,log2(2-x)取正号或负号的条件,而其中对x作分类讨论的全集又是由x>0,且2-x>0,决定的.
例7
解关于x的不等式: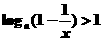
4、解简单的指数、对数不等式时,常用的方法有同底法、转化法、换元法和图象法等.
同底法:将指数、对数不等式转化为相同的底数后,再根据函数单调性进行同解变形。


转化时,不要疏忽了对定义域的要求。
换元法:多用于两边是和的形式,把原不等式换元成一元二次不等式或无理不等式等形式,或先两边取对数后换元,要注意取对数时其数必须为正,要注意新元的取值范围.
转化法:多用于指数不等式,通常对不等式两边取同底对数,转化为对数不等式.要注意转化的等价性.
3、解含有绝对值符号的不等式关键是正确地脱去绝对值符号,转化为有理不等式再求解,常见的转化有:
(1)|f(x)|<g(x) (g(x)>0)Û-g(x)<f(x)<g(x)
(2) |f(x)|>g(x) (g(x)>0)Ûf(x)<-g(x)或f(x)>g(x)
(3) |f(x)|<|g(x)|Û f2(x)<g2(x)
或|f(x)|>|g(x)|Û [f(x)+g(x)][ f(x)-g(x)]>0
含有多个绝对值的不等式,可采用“零点分区间”法求解.利用绝对值的几何意义解含有绝对值符号的不等式,也是一种简便的方法.此外,借助函数图象也是一种好方法.

 的解集为(
).
的解集为(
).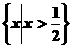 B.
B.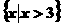
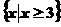 D.
D.
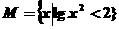 ,则M等于(
)
,则M等于(
)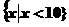 B.
B.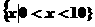
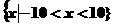 D.
D.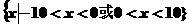
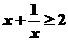 的解集为(
).
的解集为(
).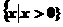
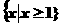 D.
D.
 同解的是(
).
同解的是(
). D.lg(x-2)£0
D.lg(x-2)£0


