21.(本小题满分12分)
双曲线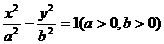 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为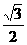 ,其中A(0,-b),B(a,0).
,其中A(0,-b),B(a,0).
(I)求双曲线的标准方程;
(Ⅱ)设F是双曲线的右焦点,直线l过点F且与双曲线的右支交于不同的两点P、Q,点M为线段PQ的中点. 若点M在直线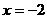 上的射影为N,满足
上的射影为N,满足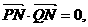
且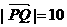 ,求直线l的方程.
,求直线l的方程.
20.(本小题满分12分)
设函数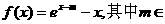 R.
R.
(I)求函数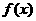 的最值;
的最值;
(Ⅱ)给出定理:如果函数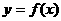 在区间[
在区间[ ]上连续,并且有
]上连续,并且有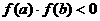 ,那么,函数
,那么,函数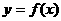 在区间
在区间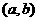 内有零点,即存在
内有零点,即存在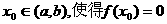 .
.
运用上述定理判断,当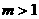 时,函数
时,函数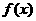 在区间
在区间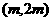 内是否存在零点.
内是否存在零点.
19.(本小题满分12分)
下表是某地一年中10天测量的白昼时间统计表(时间近似到0.1小时)
|
日期 |
1月1日 |
2月28 日 |
3月21 日 |
4月27 日 |
5月6 日 |
6月21 日 |
8月13 日 |
9月20 日 |
10月25日 |
12月21日 |
|
日期位置序号x |
1 |
59 |
80 |
117 |
126 |
172 |
225 |
263 |
298 |
355 |
|
白昼时间y(小时) |
5.6 |
10.2 |
12.4 |
16.4 |
17.3 |
19.4 |
16.4 |
12.4 |
8.5 |
5.4 |
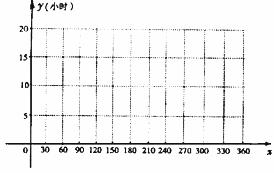
(I)以日期在365天中的位置序号x为横坐标,白昼时间y为纵坐标,在给定坐标系中画出这些数据的散点图;
(Ⅱ)试选用一个形如 的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
(Ⅲ)用(Ⅱ)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
18.(本小题满分12分)
正四棱柱ABCD-A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,
 .
.
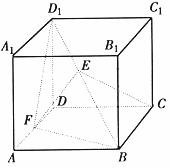
(I)建立适当的坐标系,求出E点的坐标;
(Ⅱ)证明:EF是异面直线D1B与AD的公垂线;
(Ⅲ)求二面角D1-BF-C的余弦值.
17.(本小题满分12分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0-5 |
6-10 |
11-15 |
16-20 |
21-25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(I)每天不超过20人排队结算的概率是多少?
(Ⅱ)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,请问该商场是否需要增加结算窗口?
16.若函数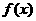 满足:
满足:
对于任意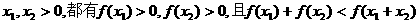 成立,则称函数
成立,则称函数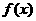 具有性质M.
具有性质M.
给出下列四个函数:①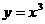 ,②
,②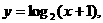 ③
③ ,④
,④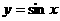 .
.
其中具有性质M的函数是 .
(注:把满足题意的所有函数的序号都填上)
12.如图,南北方向的公路l,A地在公路的正东2km处,
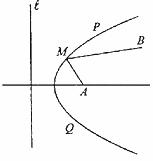 B地在A地东偏北30°方向2
B地在A地东偏北30°方向2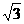 km处, 河流沿岸
km处, 河流沿岸
PQ(曲线) 上任一点到公路l和到A地距离相等.现
要在曲线PQ上选一处M建一座码头,向A、B两地
转运货物,经测算从M到A, M到B修建公路的费
用均为a万元/km,那么修建这两条公路的总费用最低
是 ( )
A.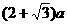 万元 B.
万元 B. 万元
万元
C.5a万元 D.6a万元
第Ⅱ卷(非选择题,共90分)

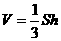 . 已知正三棱锥P-ABC底面边长为2
. 已知正三棱锥P-ABC底面边长为2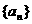 中,已知
中,已知
 =
.
=
.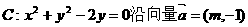 平移后得到圆C′,且C′与直线
平移后得到圆C′,且C′与直线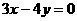 相切,则m的值为 .
相切,则m的值为 .