
科目: 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目: 来源: 题型:
【题目】某房地产开发商有一块如图(1)所示的四边形空地ABCD,经测量,边界CB与CD的长都为2km,所形成的角∠![]() .
.
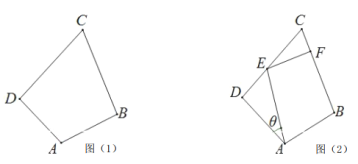
(I)如果边界AD与AB所形成的角![]() ,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
(II)当边界AD与CD垂直,AB与BC垂直时,为后期开发方便,拟在这块空地上先建两条内部道路AE,EF,如图(2)所示,点E在边界CD上,且道路EF与边界BC互相垂直,垂足为F,为节约成本,欲将道路AE,EF分别建成水泥路、砂石路,每1km的建设费用分别为![]() 、a元(a为常数);若设
、a元(a为常数);若设![]() ,试用
,试用![]() 表示道路AE,EF建设的总费用
表示道路AE,EF建设的总费用![]() (单位:元),并求出总费用
(单位:元),并求出总费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E,Q分别是BC和PC的中点.
,E,Q分别是BC和PC的中点.
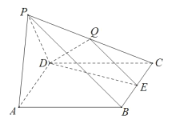
(I)求直线BQ与平面PAB所成角的正弦值;
(Ⅱ)求二面角E-DQ-P的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其上顶点为
,其上顶点为![]() ,右顶点和右焦点分别为
,右顶点和右焦点分别为![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),
),![]() ,试判定直线
,试判定直线![]() 是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为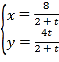 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com